本文是《试验设计》:试验精度的续篇,用同样的分析框架重新解读《实验员的统计学》中的2³完全析因试验案例。如果您对试验设计(DoE)感兴趣,欢迎关注公众号。
一句话总结《试验设计》:试验精度中的分析框架:对于随机化区组试验,依次计算残差 –> 残差表 –>残差的标准差 –> 效应(均值差)的标准误 –> 显著性检验(t检验,置信区间,68/95/99/7法则及其图形化表达),目标是判断水平之间、区组之间是否存在显著性差异。
本文使用同样的分析框架,重新解读【摘抄】《实验员的统计学》:5.7 真实的重复试验中的2水平完全析因试验;目标是回顾和加深理解DoE中的”试验精度”。
两个案例的异同,见下表:
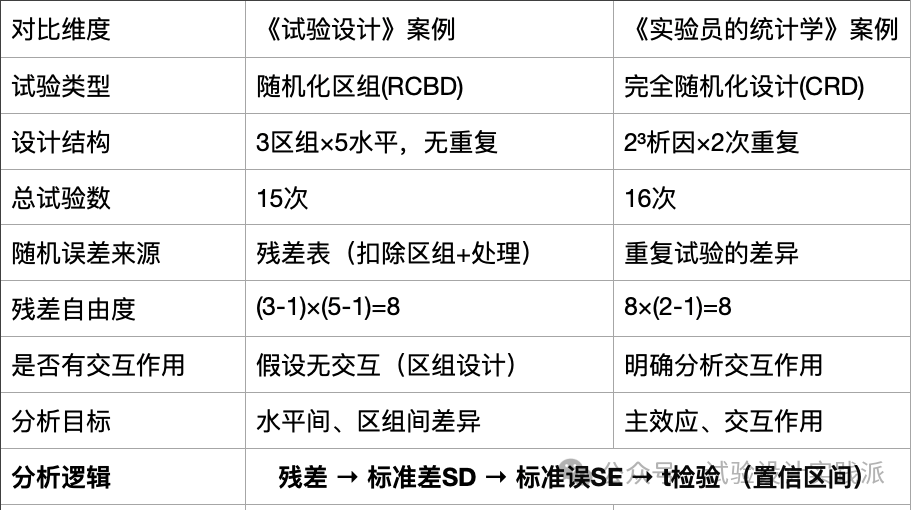
分析目标看似不同,但分析逻辑完全一样。在两水平试验中,水平之间的差异就是效应值,因此”判断水平差异”等价于”判断效应显著性”。
值得单独强调的是,两个案例都使用t检验(以及图形化分析),而非ANOVA方差分析,以后展开分享两者的差异(核心答案在【摘抄】《实验员的统计学》:5.7 真实的重复试验)
第一步:总的试验间变异s²(the total run-to-run variability)
通过真实的试验重复,我们的意思是说:在相同试验条件下所做的试验之间的差异,是所有试验与试验之间差异的一个反映。By genuine run replicates we mean that variation between runs made at the same experimental conditions is a reflection of the toral run-to-run variability. 《实验员的统计学》
这是一个经典的DoE案例:三因子两水平完全析因试验,8个处理(试验组合),每个处理2次重复,总共16次试验。
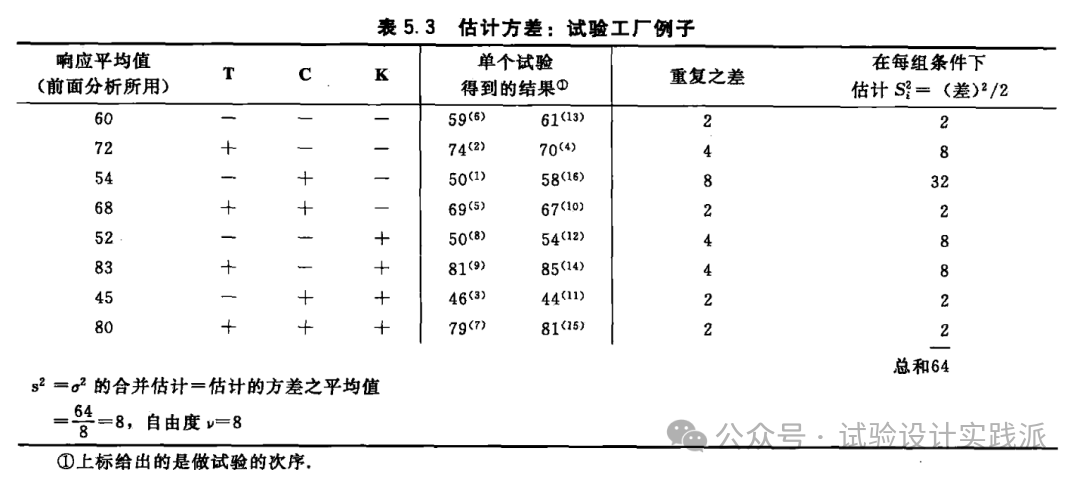
表5.3首先计算了”重复试验的差异”,首先列出每对重复的差值 d,然后使用公式 s² = d²/2 计算每对的方差估计。【原因下面解释】
然后计算8对重复的合并方差(pooled variability),因为s² = [Σ(d²/2)] / g,抽样量g=8,所以:s² = 64/ 8 = 8
备注:这不是基于中心极限定理,而是多个独立方差估计的平均。
观察表 5.3 中从 8 个不同因子组合得到的 8 对观测值。从每个重复试验的差 d 可以得到一个自由度为 1 的方差估计:s² =d²/2。这些单自由度估计的平均值产生一个自由度为 8 的合并估计:s² = 8.0。
备注1:关键公式 s²=d²/2 的快速推导:
-
假设一对观测(y₁, y₂)
-
均值 ȳ = (y₁+y₂)/2
-
残差1 = y₁ – ȳ = y₁ – (y₁+y₂)/2 = (y₁-y₂)/2 = d/2
-
残差2 = y₂ – ȳ = y₂ – (y₁+y₂)/2 = (y₂-y₁)/2 = -d/2
-
方差 = [(d/2)² + (-d/2)²] / 1 = d²/2
备注2:与残差表的等价性
本案例首先利用“重复之差d”估计s²,然后计算合并方差;而《试验设计》:试验精度首先列出试验残差表,然后一步计算残差的标准差。
两个计算过程是等价的,如下所示,都是计算残差方差。Box的方法只是利用了”两次重复”这一特殊情况的简化形式。

比如我们可以直接绘制出该试验的残差图,如下所示:
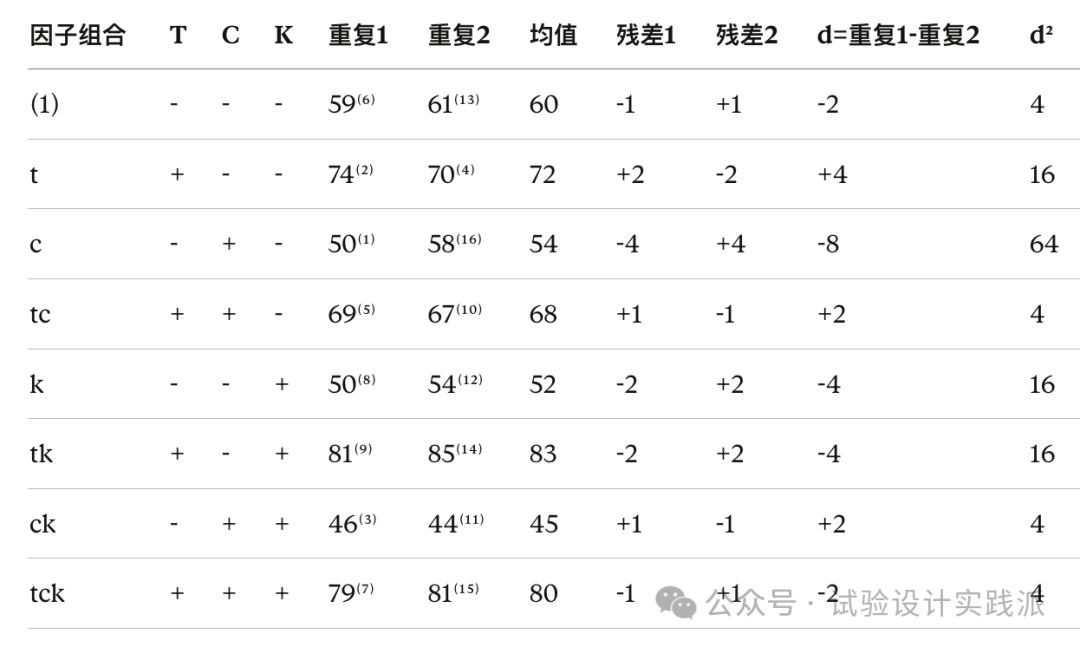

因此,对于两水平两次重复试验,绘制残差表并计算标准差,不如用s² =d²/2简洁(就像作者推荐用t检验而非方差分析)。
第二步:效应(均值差)的标准误(standard error,SE)
我们已经得到了总试验的方差估计s²=8,但是我们真正需要的是效应的标准误差SE。
从标准差到标准误的计算逻辑:
1. 效应是两个均值之差。–> 参考“平均值之差的标准误差的计算公式(文末截图)”
2. 均值是一个样本统计量,是n个样本(观测值)的平均值。均值的方差 ≠ 观测值的方差。基于中心极限定理,n个观测的均值的方差:s²/n
因为每个估计的效应(T、C、K、TC、……)是 8 个观测的两平均值之差,所以一个效应的方差为:
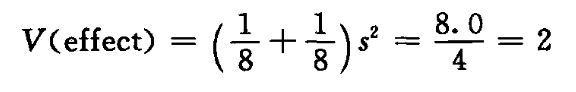
它的平方根是一个效应的标准误差:SE(effect) = 1.4
第三步:结果的解释:效应 ± 标准误差
有了效应的标准误差,就可以判断各个效应是否显著。
标准误的应用:“在任意指定的概率水平下,从观测结果中确定对照的真实值所处的范围”。
粗略规则:68/95/99.7法则——分别对应±1倍、2倍和3倍标准误差的置信区间
在大约1/3的情况下,估计值的误差将超过正负一个标准误差;
在大约1/20的情况下,估计值的误差将超过正负两个标准误差;
在大约1/100的情况下,估计值的误差将超过正负2.5个标准误差。
《试验设计》
样本量少时,需要基于残差自由度修正。
本案例中
-
残差自由度为8,
-
95%置信水平:t₀.₀₅,₈ = 2.31(而非2)
-
95%置信区间:效应 ± 2.3倍标准误差(而非2倍标准误差)。
如果置信区间不包含0,则该效应几乎肯定(almost certainly)不是来自噪声的,是真实的。

试验工厂数据的所有估计效应及其标准误差都在表 5.4 中列出了。重要的是需要找到一种方法,用来确定哪些效应几乎肯定是真实的,哪些效应容易用机会变异来解释。(which effects are almost certainly real and which might readily be explained by chance variation.)
一个粗略的规则是:2 倍或 3 倍其标准误差的效应不容易仅仅用机会变异来解释。
更精确地,在 NIID 假设下,每个比值effect/SE(effect)将服从自由度为 𝑣 = 8 的 t 分布。在 5% 显著性水平下,t 的显著值为 2.3,即:Pr(|t8| > 2.3) = 0.05;这样,对表 5.4 中的一个效应,95% 置信区间应该是:±2.3 * 1.4(即 ± 3.2)。我们更喜欢给出估计的效应及其标准误差(像本例在表 5.4 中给出的那样),而把对任一置信区间显著性水平的选取留给读者来判断。
在表 5.4 中,几乎肯定不是来自噪声的效应显示为黑体。
第四步:解读显著的交互作用
之前强调过交互作用的重要性,比如交互作用会导致明显的复杂性(非线性),是DoE相比于OFAT的核心优势之一,“OFAT的最大缺点在于,它没有考虑因子间可能存在的交互作用”。
完全析因试验可以轻松研究交互作用,正如本案例中可以分析交互作用是否显著,并识别出温度T和催化剂K之间存在明显的交互作用——这或许就是专家的直觉,但在DoE中可以被量化。
从两向图(a)可以看出:催化剂A:低温→高温,产量从57.0→70.0,增加13;催化剂B:低温→高温,产量从48.5→81.5,增加33。
TK交互作用 = [(温度效应在B) – (温度效应在A)] / 2 = (33.0 – 13.0) / 2= 10
图(b)用不同斜率更直观地展示了两种催化剂对温度响应的巨大差异。
如果有证据表明存在一个或者多个交互作用,就必须把有关交互作用的变量放在一起考虑。
温度和催化剂类型有交互作用。
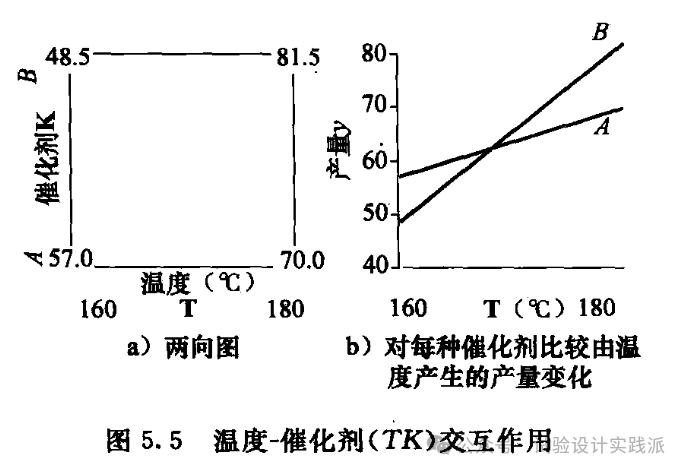
在本例中,实际上最令人感兴趣的结果是两种不同的催化剂响应温度的表现竟然那么不同。该影响是预想不到的,
延伸思考:完全重复是“奢侈”的吗?
本案例采用完全重复,16次试验 = 8个组合 × 2次重复,其中8次是为了估计s²(试验精度)。
作者提到,“像这里所做的将 2^3 因析设计完全重复外,还有更好的方法来安排 16 次试验”,这也是无重复析因试验怎么分析?——摩托罗拉波焊案例的延伸思考所表达的观点。
重复试验是估计精度的最直接方法,但不是唯一方法。真正明白了试验精度的本质和计算方式,就可以更灵活地设计试验,比如利用部分重复,利用高阶交互作用估计误差(效应稀缺原理),基于历史数据或专家经验等计算试验精度。
《实验员的统计学》给出了一个“部分重复“的案例,感兴趣的可以找一下~
参考资料:平均值之差的标准误差的计算公式
《实验员的统计学》第3章 比较两总体:参照分布、检验和置信区间

合并方差的计算:

欢迎点赞👍、推荐❤️、分享📣、留言✉️;
学习、实践、只为解决问题!
🧧 预祝大家2026年春节快乐!阖家幸福,龙年大吉! 🎊
