第一个方面,可以投入到试验中的努力程度可能会受到实验者无法控制的情况的限制。此时,在进行试验之前对可能产生的精度进行一些粗略的估计几乎总是有益的。例如,此粗略估计可以表明最终估计很可能会出现很大的误差,以至于无法得出有效的结论,因此建议,除非可以集中更多的资源,否则该试验不值得做。或者看上去可以用少于全部试验单元的数量获得足够的精度。
第二个方面是较积极的,如果单元数量在很大程度上可由实验人员掌控,则我们可以计算出与单元数量值范围相对应的精度。因此就可以达到以下两种情况之间的合理折中:其一是过少的单元数量和过低的精度,其二是浪费时间和试验材料来获得不必要的精度。
《试验设计》p105
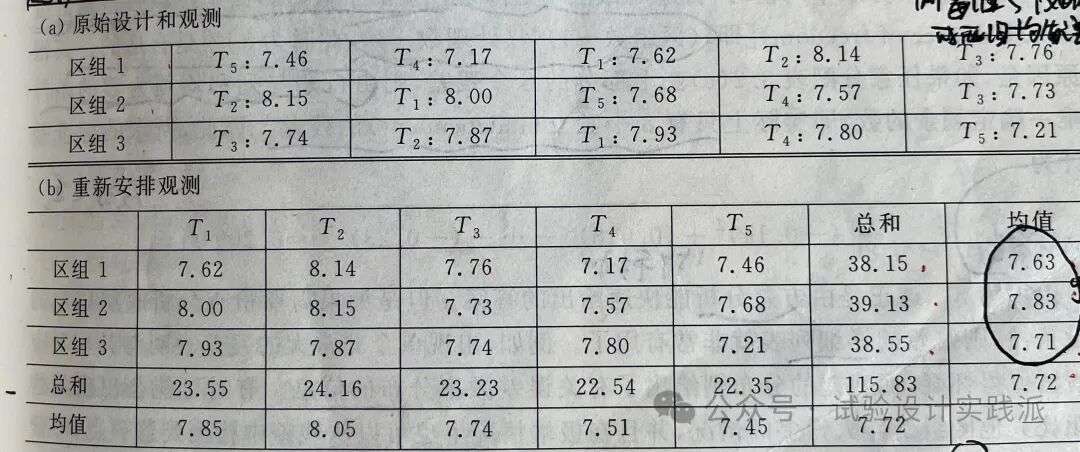
例3.2 在 Cochran 和 Cox(1957,4.23 节)讨论的一项试验中,有三个区组,每个区组包含五个地块。处理方法是在三个区组的每英亩棉花地上分别施用五个水平的钾肥:36、54、72、108 和 144磅(lb)。观测值(响应值)是单纤维强度,通过对每个地块上的棉花多次测试后取平均值。原始结果及区组均值、处理均值如下表。
在试验的每个阶段,不可控变异的来源中的任何一个,要么用区组来标识,实际上就从处理对比中被消除了,要么被随机化,要么可能被认为是可忽略不计的。尽可能避免最后一项,因为如第1章所述,通常最好避免对不可控变异的属性进行假设。 《试验设计》p19
我们需要测量的随机变异不是由实际处理效应引起的,也不能被视为区组之间的系统性变化。因此,很自然地首先应将每个观测表示为与总体均值的差异,然后消除由区组不同引起的变异。这通过以下公式完成:
(指定区组的观测均值)-(总体均值)
接着,消除由处理解释的变异
(指定处理的观测均值)-(总体均值)
在此步骤结束时,对应于每个原始观测,我们得到一个残差(residual),该残差可以直接定义为
观测 – (指定区组的观测均值) – (指定处理的观测均值) + (总体均值)
《试验设计》p20

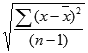
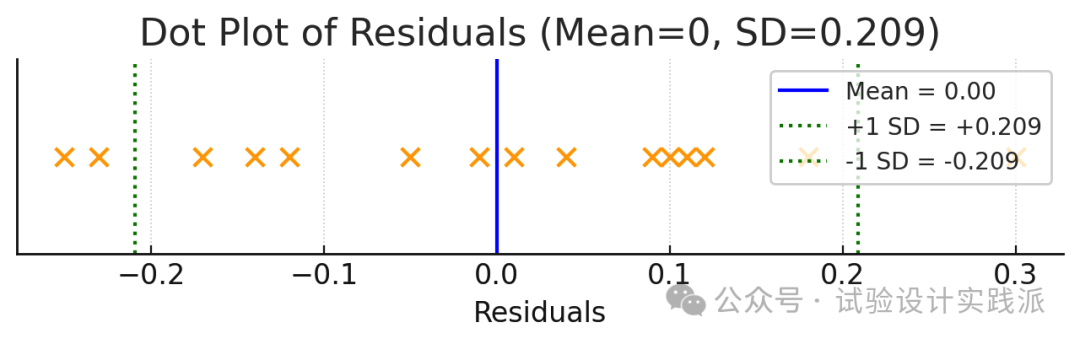
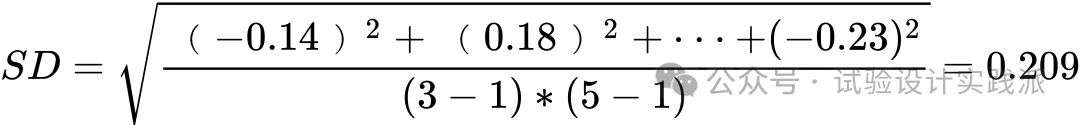
标准参度量了残差的大小,通过找到残差平方的平均值然后对其求平方根来计算得出。但是,在对残差平方求平均值时,合适的做法不是除以残差的个数(15)而是除以残差自由度(residual degree of freedom)[即(区组数-1)X(处理数-1),此时为8]才是合适的。其根本原因是,如果任意分配表3.2(c)左上部分的8个残差,则由行和与列和均须为零的条件将唯一确定剩余的数,即实际上只有8个独立(independent)的残差。
《试验设计》p20
“试验的精度,是该试验的随机误差的大小。”这句话不够“精确”,因为残差量化了试验误差(experimental error),残差标准差量化了残差的离散程度(spread),但我们依然不知道试验的精度的高低。
通常使用标准误差(standard error,SE)来度量随机误差的大小!
《试验设计》
The standard deviation of the average, s/√n, is the square root of the variance of the average, and is referred to as the “standard error”of the average.The square root of the variance of any statistic constructed from a sample of observations is commonly called that statistic’s standard error. 《statistics for experimenters》
如果每个试验单元观测到一个观测值,则在其他条件相同的情况下,两种处理之同差异估计值的标准误差与每种处理的单元个数的平方根成反比。实际上,标准误差为

若A、B两种处理得到的观测个数不同,则为

这里的标准差(standard deviation)是经过相同处理的试验单元上的观测值的随机散度的统计量度。p6
回到例3.2,两个处理(即两个水平,每组重复3次)之间的标准误差:

按照同样的方式,可以计算出两个区组(每个区组重复了5次)之间的标准误差:

有了(均值差的)标准误,就可以比较均值差的差异是否显著——五个水平之间的两两比较,以及三个区组之间的两两比较。
具体的比较方法,可以是t检验或F检验,最好是结合图形化比较。
《试验设计》提供了一种最简单但也最体现标准误本质的方法——68/95/99.7法则,同时也解释了标准误差的在应用层面的含义。
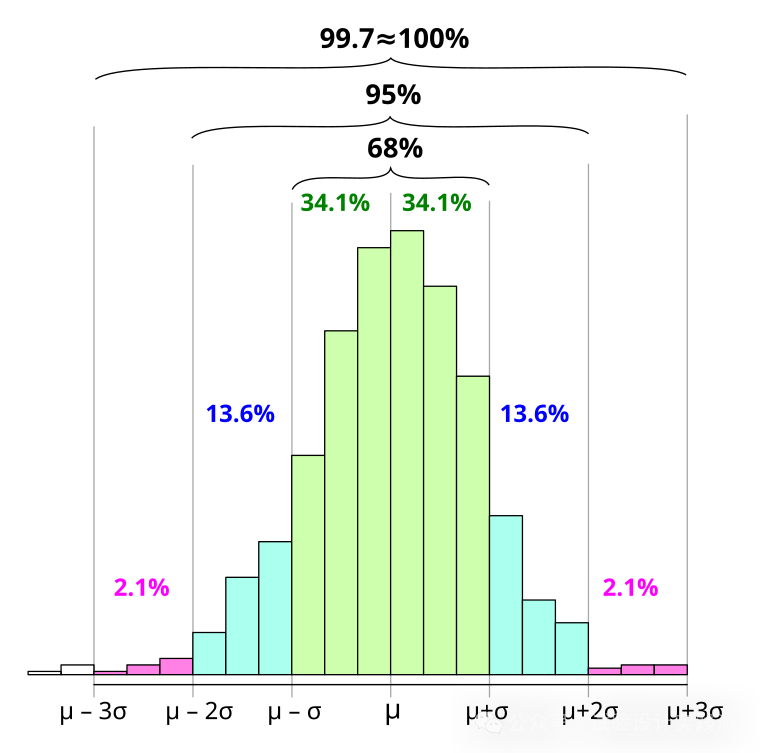
在大约1/3的情况下,估计值的误差将超过正负一个标准误差;
在大约1/20的情况下,估计值的误差将超过正负两个标准误差;
在大约1/100的情况下,估计值的误差将超过正负2.5个标准误差。
《试验设计》p5
回到例3.2,两个处理(即两个水平)之间的标准误差为0.171,如果两个均值差超过0.395(t调整),那只有1/20=5%的概率是偶然因素所致。
因此,T2(最大值)和T5(最小值)之间,T2(最大值)和T5(次小值)之间,T1(次大值)和T5最小值)之间,都存在显著性差异(p<0.05)。换言之,当前的试验精度,足以区分五个水平之间的部分差异。——图形化表达会更直观一些,我就先跳过了。
对于预先选定效应的估计,其误差超过 ±2*0.171=±0.342的概率仅约1/20。但是,当标准差本身仅是根据少量观测值估计得出时,需要对这种解释进行一些修型,面实际上是残差自由度确定了该如何修正。当有8个自由度时,1/20的临界值应增加到2.31*标准差,即±0.395。从2 增加到 2.31,以允许误差估计中的不确定性,这在统计方面的教科书中已作了解释,是使用所谓的“Student” t分布的一个范例。p21
一般经验表明,不应将小于约5个自由度得到的标准差用于估计标准误。p113
《试验设计》
按照同样的方式,也可以对比三个区组之间的均值差是否存在显著性差异,此处略。
五、提高精度的三个办法
以上分享的内容,主要是“试验之后”的精度量化,进而判断处理之间和区组之间的差异是否显著;如果发现精度不足,简单的补救方法是增加重复次数,但增加重复不一定能明显增加精度,所以还要考虑其他的办法,特别是“试验之前”的准备工作,不论是(通过团队合作)预先了解尽可能多可能的变异来源,明确测量系统的精度,还是选择精度更高的试验类型(比如从增加区组因子)。
标准误差(standard error,SE)的取值——由此任何一个指定试验的精度–取决于:(1)试验材料的内在差异性(变异性)和试验工作的准确性;(2)试验单元的数量(以及对每个试验单元重复观测的数量);(3)试验的设计(如果效率不高,还取决于分析方法)。 《试验设计》p6
对于第一点,Cox认为“在统计设计能够提供帮助的大多数试验中,改进试验材料或提高测量设备的精度只能实现非常有限的精度提高”;第一点应该是试验设计的前提,即试验前明确试验材料和测试系统中的可能变异来源及其控制方法。
对于第二点,即试验设计的第三个原则——”重复试验”或”观测数量”,我们可以在试验前粗略地估算试验精度,避免试验产生很大的误差以至于无法得出有效的结论等风险;当然也可能精度过高,则需要适当减少试验单元的数量。
对于第三点,则是试验设计的策略性。合理的试验设计,有可能达到与大规模增加试验单元数量相当的精度提高;这就是试验设计的魅力所在。 比如第7章 “水平的选择”介绍了如何选择合适的水平的数量和位置,控制精度,避免了盲目增加试验量而没有明显提高精度的情况。
如何确保不可控变异尽可能少的干扰结论:我们可以通过将试验单元分组为随机区组或拉丁方,或使用基于伴随变量的调整,来减少某些变异来源的影响,并且可以通过随机化将剩余变异转化为实际上的随机变异。 《试验设计》p97
不论是哪种控制精度的方法,都是控制试验误差SE的方法。
如果本文对你有所启发,欢迎点赞👍、推荐❤️、分享📣
学习,实践,解决问题!
