《试验应用统计》(Statistics for Experimenters,实验员的统计学)
作者:George Box, J. Hunter, William Hunter

第5章 “两水平因析设计”
-
5.7 真实的重复试验
-
5.8 结果的解释
结合本文的案例,我会单独整理一篇学习笔记,再次分享如何计算”效应的标准误差”,以及和《试验设计》:试验精度的异同点。
2. 计算两个试验结果的方差,简洁计算公式:s² =d²/2(可以从标准的方差计算公式换算过来)。,这个公式常用于两水平析因试验,后面有一段内容提到的N*(Effect)^2/4就是利用了这个结论。
考虑一个有k个因子n次重复的两水平的设计,它共进行了 N = n * 2^k 次试验,在 ANOVA 分析中,处理的 2^k – 1 个自由度被分成单个效应的平方和,它等于 N*(Effect)^2/4。
5.7 真实的重复试验 Genuine Replicate
尽管通常有使用 16 次试验的更好方法,但表 5.2 中的 8 个响应是表 5.3 中相应的两次真实重复试验的平均值。通过真实的(genuine)试验重复,我们的意思是说:在相同试验条件下所做的试验之间的差异,是所有试验与试验之间差异的一个反映。(By genuine run replicates we mean that variation between runs made at the same experimental conditions is a reflection of the toral run-to-run variability)这一点需要仔细考虑。
所有 16 次试验顺序的随机化(如表 5.3 所示)确保了重复是真实的。但是,重复试验并不总是容易做到的。对该试验工厂的试验,一次试验包括:(1)清洗反应器;(2)加入适量的催化剂;(3)在给定的温度和浓度下让机器运行 3 小时,使过程稳定在选定的试验条件;以及(4)在运行的最后时间内,每隔 15 分钟抽取一次样本。一次真实的试验重复包括将所有这些步骤全部再做一次。特别地,仅对单个处理组合抽取单个样本的化学分析进行重复,只能提供分析方差的一个估计,这通常只是试验处理组合和处理组合方差中很小的一部分。类似地,来自同一处理组合的重复样本仅可以提供抽样和分析方差的一个估计。为了得到可以用来估计某个特定效应标准误差的误差估计,每次试验处理组合必须真实地重复。对试验误差方差的错误评估问题是很麻烦的,这将在第 12 章中更全面地进行讨论。
试验中的节俭 Economy in Experimentation
通常,除了像这里所做的将 2^3 因析设计完全重复外,还有更好的方法来安排 16 次试验。在后面你会看到,怎样可以在一个 16 次试验的两水平设计中考察 4 个或者 5 个(有时甚至更多)因子,而不需要重复试验。不需要重复试验的效应显著性评估也会在后面讨论。而现在仍然是考虑重复数据的分析问题。
来自重复试验的误差方差和效应的标准误差的估计
Estimate of the Error Variance and Standard Errors of the Effects from replicated Runs
观察表 5.3 中从 8 个不同因子组合得到的 8 对观测值。从每个重复试验的差 d 可以得到一个自由度为 1 的方差估计:s² =d²/2。这些单自由度估计的平均值产生一个自由度为 8 的合并估计:s² = 8.0,因为每个估计的效应(T、C、K、TC、……)是 8 个观测的两平均值之差,所以一个效应的方差为:
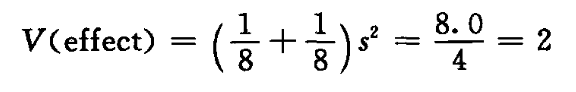
它的平方根是一个效应的标准误差:SE(effect) = 1.4
一般来说,如果每个因子组合都重复,那么 g 个因子组合的试验方差的一个合并估计是:
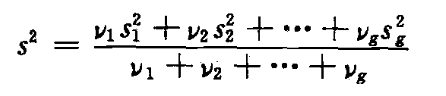

5.8 结果的解释
试验工厂数据的所有估计效应及其标准误差都在表 5.4 中列出了。重要的是需要找到一种方法,用来确定哪些效应几乎肯定是真实的,哪些效应容易用机会变异来解释。一个粗略的规则是:2 倍或 3 倍其标准误差的效应不容易仅仅用机会变异来解释。更精确地,在 NIID 假设下,每个比值effect/SE(effect)将服从自由度为 𝑣 = 8 的 t 分布。在 5% 显著性水平下,t 的显著值为 2.3,即:Pr(|t8| > 2.3) = 0.05;这样,对表 5.4 中的一个效应,95% 置信区间应该是:±2.4 * 1.4(即 ± 3.2)。我们更喜欢给出估计的效应及其标准误差(像本例在表 5.4 中给出的那样),而把对任一置信区间显著性水平的选取留给读者来判断。
在表 5.4 中,几乎肯定不是来自噪声的效应显示为黑体。

待估效应表的说明
只有当没有证据表明某因子与其他因子有交互作用时,该因子的主效应才应该单独解释。如果有证据表明存在一个或者多个交互作用,就必须把有关交互作用的变量放在一起考虑。在表 5.4 中可以看到,有一个很大的温度主效应 23.0 ± 1.4,但是不应该就此得出温度单独起作用的结论,因为温度和催化剂类型有交互作用(TK 交互作用的值为 10.0 ± 1.4)。然而,对浓度的情形,主效应为 -5.0 ± 1.4,并且没有证据表明它和其他因素有交互作用。于是可以得到下面试验性的结论:
1. 浓度(C)在试验研究范围内改变的效应是将产量降低大约 5 个单位,而且这和其他变量的检验水平近似地无关。
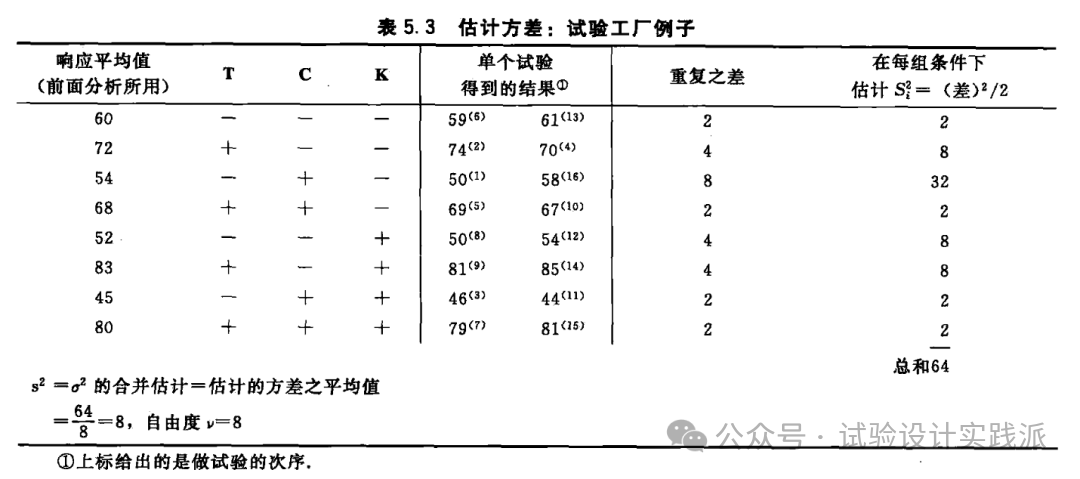
2. 温度(T)和催化剂(K) 的效应不能分开解释,因为它们的交互作用 TK 非常大。在催化剂为 A 的情况下,温度的效应是 13 个单位;但是在催化剂为 B 的情况下,温度的效应为 33 个单位。可以通过研究图 5.5a 中的两向图来理解交互作用。等价地,图 5.5b 展示出交互作用是如何由两种催化剂对温度的灵敏度差别而产生的。
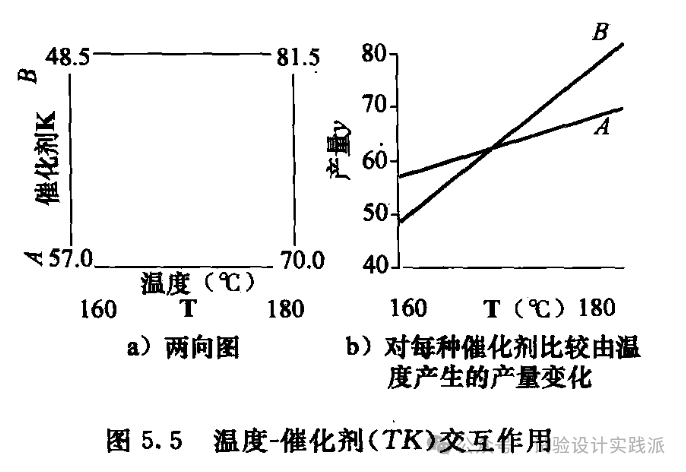
在本例中,实际上最令人感兴趣的结果是两种不同的催化剂响应温度的表现竟然那么不同。该影响是预想不到的,因为尽管两种催化剂是从不同供应商处得来的,但是它们按照推测是相同的。同时催化剂为B、温度为180℃时的产量目前看起来是最高的.这个发现引导我们在后续调查中要仔细考虑催化剂和催化剂的供应商问题.
5.10 2^k因析试验中ANOVA的误用
Misuse of the ANOVA for 2^k Factorial Experiments
很多电脑程序都利用 ANOVA(方差分析表)来分析2^k设计(和它的部分设计,见第6 章),但是分析这种特殊的设计时,使用ANOVA 会非常令人费解,并且没什么意义,考虑一个有k个因子n次重复的两水平的设计,它共进行了 N = n * 2^k 次试验,在 ANOVA 分析中,处理的 2^k-1 个自由度被分成单个效应的平方和,它等于 N*(Effect)^2/4,每个都除以它自己的自由度得到均方。这样就看不到效应本身,试验者只看到 N*(Effect)^2/4,进而去查自由度为1的F分布表,没有方法证明这种复杂的做法,也不能证明对ANOVA 的普遍价值的盲目相信。试验者想知道的是效应的大小、它的标准误差和比值 t=Effect/SE(effect)。
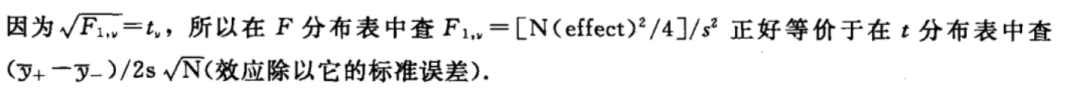
大部分电脑程序在5%和1%概率水平下计算原假设下的p值。p值不能被机械地用来判断哪个效应是真的,哪个效应是可以忽略的。在对统计方法的合理利用中,效应大小及其可能误差的信息必须和试验者的专业知识相结合。(如果有p=0.50的概率可以在下一棵树后面找到一瓦罐金子,你不愿走过去看看吗?)即将讨论的图形方法为让数据的信息和试验者心中的经验适当地结合提供了一种有价值的方法.