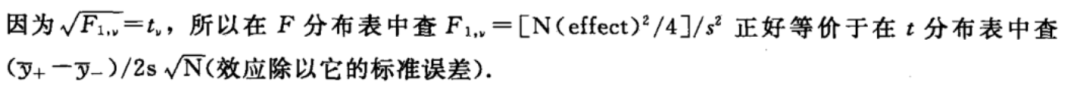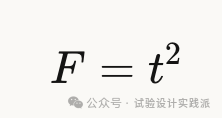两水平析因试验：多用t检验，少用ANOVA方差分析

本文分享我阅读《实验员的统计学》（Statistics for Experimenters，中译本：试验应用统计）的一个关键收获，文末附原文摘抄。
我们做两水平析因试验时，习惯于使用软件自动生成的ANOVA方差分析表，使用p值判断效应是否显著。但统计大师George Box在《实验员的统计学》中提出一个建议：
对于两水平析因试验，应该多用t检验，少用ANOVA方差分析。
因为两个关键原因：
  1. 对于两水平析因试验，t检验和ANOVA方差分析是等价的（equivalent）；
  2. “t检验有更直观的物理含义”。

一、为什么“t检验有更直观的物理含义”

1.1 t值的本质：信噪比

首先，t值是一个统计量（回顾DoE基础：为何是“参数检验”而非“统计量检验”？）；
其次，”t值度量的是工程师们熟悉的信噪比”（measures the signal-to-noise ratio）；
再次，使用t值进行显著性检验，目的是”表面上的信号能否被噪声所解释”（the significance test tells you if the apparent signal could or could not easily be explained by the noise.）——呼应上面的信噪比；
最后，在标准的析因试验设计中，实验者使用t值判断效应值（Effect）是否显著，计算公式如下：
t=Effect/SE(effect)
这个公式的物理含义非常清晰：
  • 分子(Effect): 我们想检测的”信号”——因子对响应值的影响（回顾DoE基本术语中对效应（Effect）的定义）
  • t值：效应大小和标准误差的比值，信号与噪音的比值，即信噪比。
信噪比是一个足够直观的概念：如果某个因子变化带来的效应远大于重复试验的随机波动，说明该因子的影响是真实的。反之，如果效应淹没在噪声中，可能只是偶然波动。

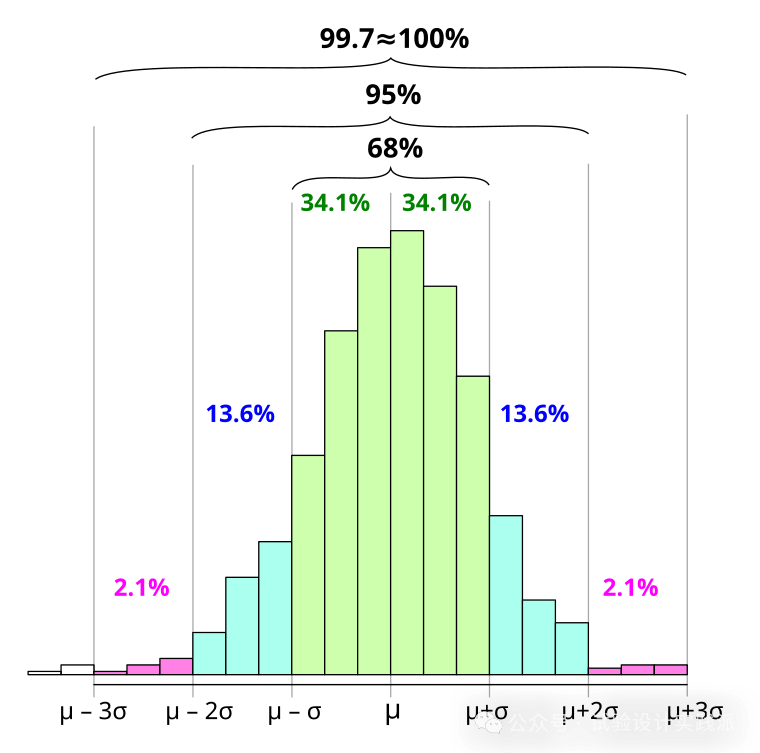
1.2 实用的68/95/99.7法则

有了t值，就可以直接使用“68/95/99.7法则”：

  • 有1/3（68%）的概率，估计值落在均值± 1个标准误差的范围内；

  • 有1/20 （95%）的概率，估计值落在均值± 2个标准误差的范围内；

  • 有1/100 （99%）的概率，估计值落在均值± 2.5个标准误差的范围内。

George Box的经验法则：超过其标准误差 2 倍或 3 倍的效应，很难仅用随机变异（偶然性）来解释。（A rough rule is that effects greater than 2 or 3 times their standard error are not easily explained by chance alone.）
图片
注意，68/95/99.7法则针对理想化的正态分布（Z检验）。实际使用t检验时，要根据实际抽样量修正。例如在《实验员的统计学》试验精度：两水平完全析因设计中，95%置信水平：抽样量和自由度为8，t₀.₀₅, ₈ = 2.31，而非2。

1.3 DoE中如何使用t检验

首先，试验者计算出效应的大小、它的标准误差和比值 t=Effect/SE(effect)；
然后，实验者结合自己的专业经验选择合适的p值（0.01，0.05甚至更高），计算出效应的置信区间（confidence interval，CI）；
最后，判断显著性，比如在之前两篇”试验精度”的两篇文章：
  • 《试验设计》：试验精度（随机化区组试验）：两个处理（即两个水平）之间的标准误差为0.171，如果两个均值差超过0.395（t调整，2.31倍标准误），那只有1/20=5%的概率是偶然因素所致。因此，T2和T5之间，T1和T5之间，都存在显著性差异（p<0.05）
  • 《实验员的统计学》试验精度：两水平完全析因设计：温度的主效应为23.0，有95%的概率，主效应落在23.0±2.3*1.4的置信区间中，不会包含0，因此温度是显著的。同理，二交互作用TK也是显著的。即使放宽到99%的置信水平，主效应T和二交互作用TK依然是显著的。
    图片
另外t检验不仅限于分析效应值，还可以分析模型系数等其他统计量。

二、在两水平析因试验中，为什么t检验和F检验是等价的？

这个有趣的结论是我阅读《实验员的统计学》的一个重大收获，之前只悟到了“t和F值都是度量信噪比的统计量”，但没有意识到两者的之间的数学关系：
图片

2.1 数学关系

对于两水平因子(自由度=1)，存在严格的数学关系:
图片
因此:
  • t检验和F检验（ANOVA方差分析）给出完全相同的统计结论；
  • 它们只是同一事实的不同表达方式。
感兴趣的话，可以自己手动计算一下，比如高水平有3个重复数据，低水平有3个重复数据，分别计算其F值和t值；更底层的数学解释，还不是我的学习重点，以后遇到通俗易懂的解释时，再做分享。

2.2 为什么ANOVA”令人费解且没什么意义”?

Box在书中批评道：ANOVA让人费解且没什么意义（原文：confusing and makes little sense）。
假设有k个因子、n次重复的两水平设计,共N = n×2^k次试验。
ANOVA的做法:
  1. 把处理的 2^k – 1 个自由度分解成单个效应的平方和
  2. 每个效应的平方和 = N×(Effect)²/4 【注意为何平方差这样计算】
  3. 除以自由度(1)得到均方
  4. 查F分布表判断显著性
问题是，ANOVA把简单问题复杂化了
  • 你看不到效应本身(Effect)，只看到 N×(Effect)²/4；
  • 需要去查”自由度为1的F分布表”。
我的理解是，F值也反映了信噪比（两个均方的比值），但却不如t值有更直观的物理含义。所以对于两水平试验，建议使用t检验；对于更复杂的多因子多水平试验，则建议使用F检验。

三、关键提醒：不要机械地使用p值，而要结合专业知识

对于了解统计学的读者来说，这个提醒自然是老生常谈。
我们常用p=0.05，但切记不要变成绝对的规则，就像Box强调的那样：“不要机械地使用p值进行判断，效应大小及其可能误差的信息必须和试验者的专业知识（subject knowledge）相结合。”。
类似的观点，之前分享过，见显著不等于重要？——摩托罗拉波焊案例的延伸思考
关于p值，Gergo Box的提醒非常棒：
如果有p=0.50的概率可以在下一棵树后面找到一瓦罐金子，你不愿走过去看看吗？If there were a probability of p =0.50 of finding a crock of gold behind the next tree, wouldn’t you go and look？
《实验员的统计学》
Box说“把对任一置信区间显著性水平的选取留给读者来判断”，我们则要知其所以然，才能用好DoE，做好试验。
图书摘抄：【摘抄】《实验员的统计学》：5.7 真实的重复试验
图片
图片
如果本文对你有所启发，欢迎点赞👍、推荐❤️、分享📣、留言✉️；

学习、实践、只为解决问题！

🧧预祝大家2026年春节快乐，阖家幸福，马年大吉！🎊

发表回复