1. SPC概论和原理
SPC的目的:管控风险,管控变异,监控过程的稳定性(是否受控),识别特殊原因变异,尽早采取行动,
特殊原因变异和一般原因变异
控制和能力:“受控”和“稳定性”是一回事;但受控不代表有能力。
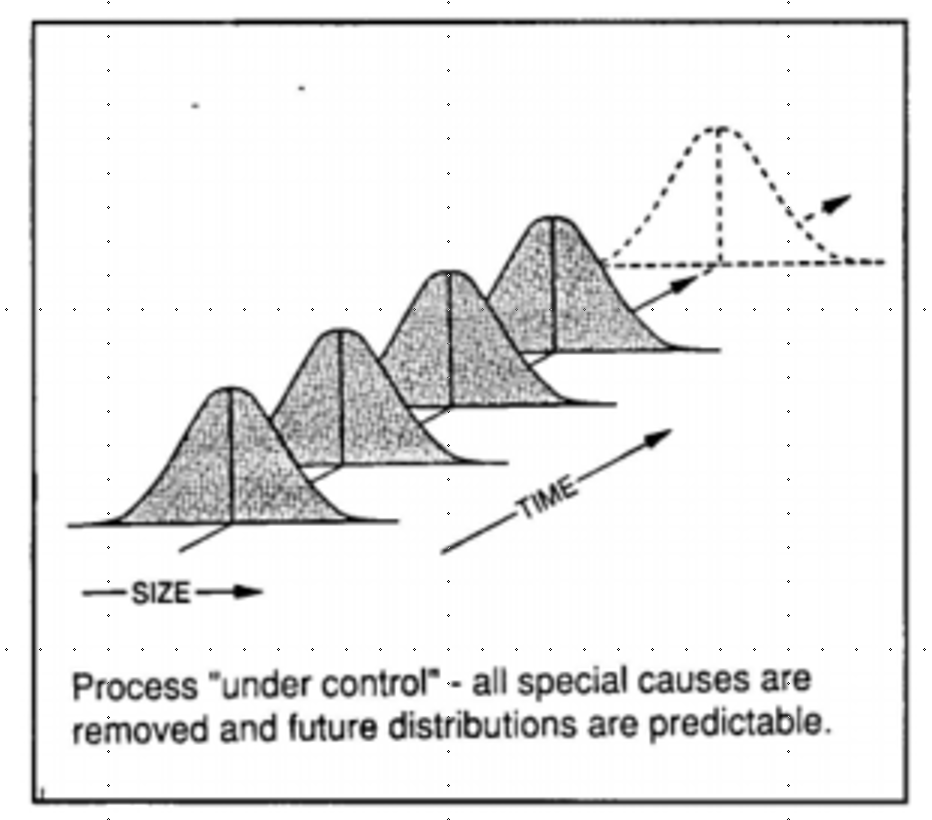
规格界限specification limits(LSL,USL)和 控制界限control limits(LCL,UCL)
规格界限反映顾客的声音,控制界限代表过程的声音。
规格界限是客户的要求,针对产品,很多x变量和衍生变量都没有规格界限(也就是不在产品spec中)。
2. 创建控制图的基本步骤
- 选择要监控的质量特性
- 确保测量系统是稳定而有能力的
- 确定取样策略
- 选择合适的控制图
- 收集数据并检验标准假设(对计量值控制图而言)
- 分析并解释数据
3. 确保过程是稳定且有能力的
SPC的前提是过程稳定,可控,没有大的系统波动,只有随机波动。
SPC的前提是,有稳定的过程能力
Cpk<1.0,没有做SPC的意义,应该全检。
Cpk在1.0-1.3之间,可以用SPC做基本的监控,但是流程还需要继续优化才行。
Cpk>1.67时,可以用SPC监控过程的稳定性,
先多抽样,做初始研究,看“初始控制图”,确定总体随时间的数据变化情况,组间波动大不大,组内波动大不大。 ——四个实例
根据波动大小,再决定选择什么样的控制图。
4. 取样策略
取样策略是步骤中比较困难的步骤,如何取样,取几个样品,课堂没有细节,暂略。
5. 如何选择合适的控制图:
要监控的质量特性,是计量型还是计数型?
取样策略,比如抽样量,选择哪种表征均值和波动的统计量,对应不同的控制图。
是否相关(是否和时间相关),是否正态
相关或独立性:控制图的取样都是随时间取样,所以样本本身不能和时间有相关性,否则就是不独立的,依赖于时间。
5.1. 计量型数据控制图:
- I—MR(单值一移动极差控制图)
- Xbar—R(均值一极差控制图)
- Xbar—S(均值一标准差控制图)
一次抽一个样本,用I-MR。
如何计算移动极差(MR,moving range):首先要定义”移动极差的长度w,默认值为2“,即只计算当前测试值和上一个结果的移动极差; 如果w=3或更大,则计算最近w个测试值的极差。 详细见 [移动极差控制图 的方法和公式 \- Minitab](https://support.minitab.com/zh-cn/minitab/help-and-how-to/quality-and-process-improvement/control-charts/how-to/variables-charts-for-individuals/i-mr-chart/methods-and-formulas/methods-and-formulas-for-moving-range-chart/#average-moving-range-method)
移动极差(Moving Range)是指两个或多个连续样本值中最大值与最小值之差。 这种差是按这样方式计算的:每当得到一个额外的数据点时,就在样本中加上这个新的点,同时删除其中时间上“最老的”点,然后计算与这点有关的极差,因此每个极差的计算至少与前一个极差的计算共用一个点的值。_ baidu
I-MR控制图: 看单值和时间的关系。
Xbar:子组数据的平均值,判断子组均值是否正态
Xbar-R和Xbar-S的区别和选择
共同点是多次抽样(一个子组),计算子组的平均值;差异是使用极差还是标准差。
S是子组平均值的标准差,R(极差,Range)是子组内的极差——两个极端样本值的差值,只看最大值和最小值。
子组数量比较少时,样本大小n恒定时,用Xbar-R; 推荐3-5个子组样本量
子组数量比较多,可以用Xbar-S, 推荐5-10个子组样本量

8个判异准则:细节略,源自假设检验和p值,即出现异常值对应的小概率事件
5.2. 属性控制图,计数型数据控制图
针对不良品,要求恒定子组,抽样结果是二项式
- Np chart :Number of Defective Units,不良品数(每次抽样次数是一样的),
- p chart:Proportion Defective,不良品率,
p图和np图,以二项式分布为基础,抽样结果是yes/no。
针对缺陷数量 ,可以是不恒定的子组
- c图:Count of Defects,缺陷数量
- u图:Number of Defects per Unit ,每一”缺陷单位“的缺陷数
c图和u图,以泊松分布为基础。


6. 收集数据并检验标准假设(计量值控制图)
比如取100多个样品,分析是否正态,是否独立。
进行独立性和正态性检验。
工作中的例子,做到rePT1时,测试胶带coating weight的cpk,要求多卷取样,首尾取样,确保数据的代表性。
7.附录内容——中心极限定理
样本量的平均值: 中心极限定理,单个样品的数据不正态,但是样本抽样的平均值,应该就是符合正态分布了。 比如每次取5-10个样品。 抽样数量,取决于总体的分布好坏,太差了就要取30个一样,如果对称性比较好(但是还不算正态分布),就建议取5-10个。
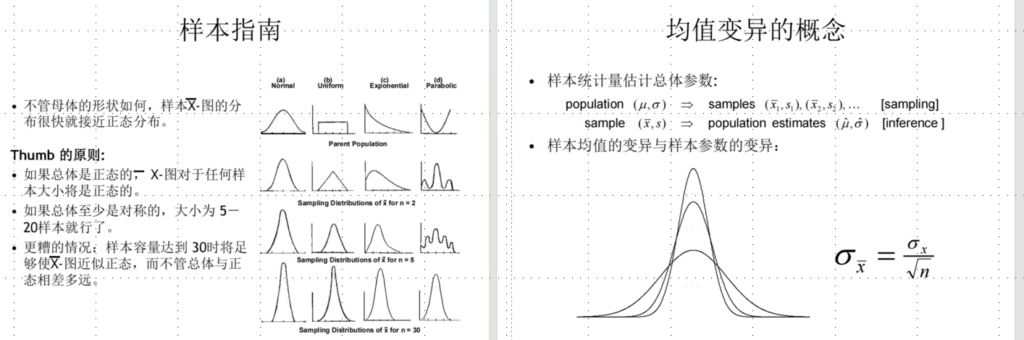
非标准假设前提下的控制图
以上都是标准假设前提,即独立(与时间无关)、正态、单一变异源;否则应该怎么做,暂略。
2024-7-14 基于21年4月和5月的课堂学习笔记,重读ppt,重新梳理一遍Control部分的主要内容。 发布