无重复析因设计在实际应用中非常广泛。[1] 本文使用摩托罗拉波焊案例,分享一些阅读和实践中的思考,即无重复(又称为单次重复、一次重复)析因试验会遇到什么问题,应该如何解决。
·为何无重复析因设计应用非常广泛?因为析因试验的处理组合总数已经很大了,比如4因子、5因子和6因子的2水平试验,分别有16、32和64个处理组合。资源总是有限的,可用的资源经常只允许做一次重复。[1]
实践中更现实的情况是,相对于增加一次完全重复,工程师(及他们的老板)更倾向于增加一个试验因子,万一被忽略的因子很重要呢,实际这样也有合理之处,后面会具体解释。
重复试验的意义
重复有两条重要的性质。第一,它允许实验者得到一个实验误差估计,这个误差估计成为一个确定数据之间的观测差是否统计意义的实际差的基本度量单位。第二,如果用样本均值(ȳ)估计实验中某一因子水平的响应均值的真值,则重复能够使得实验者得到更精确的参数估计。[1]
分享我对这两条性质的理解。第一,要得出误差平方和,至少要有两次重复。如果没有重复,纯误差的自由度为零,这称为“试验饱和”,此时无法进行方差分析(F检验)。第二,使用重复试验的平均值(即样本均值)估计该处理组合的真值,使用重复试验的波动(样本均值的标准差)估计真值的波动(标准差),对应的具体工具是“中心极限定理”(central limit theorem) ,未来再展开介绍,下面的交互作用图也会重点强调这一点。

无重复析因试验案例,问题是什么
回到摩托罗拉波焊案案例上,我们假定两次重复试验的平均值为无重复试验结果,结果整理到Design Expert中,如下表所示。
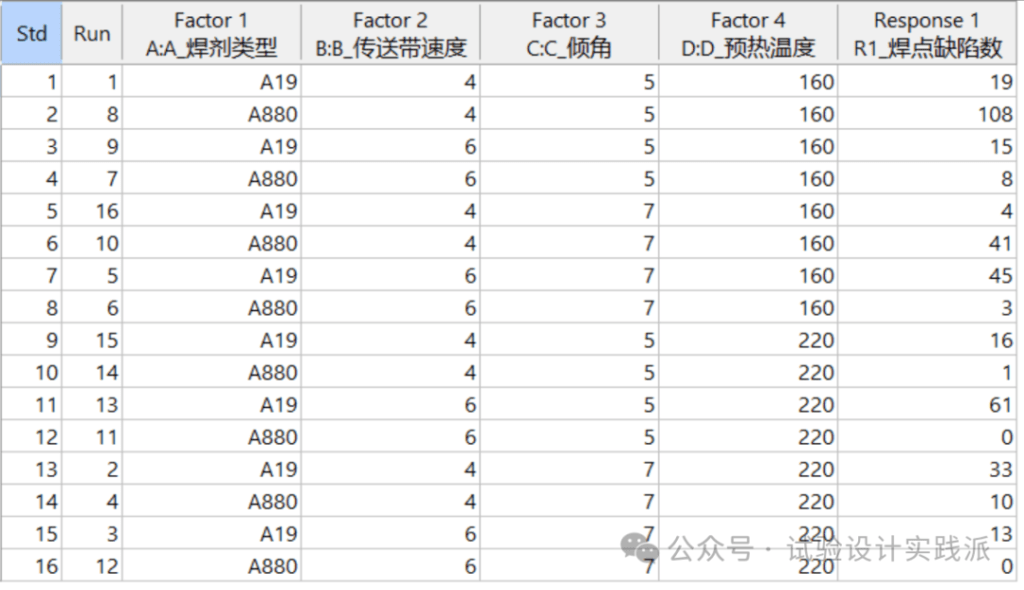
按照从定义到实践:Design Expert完全析因试验(下)的统计分析步骤(蓝色标注为细节修改),看和两次重复试验的结果有何不同
- 估计因子效应:计算主效应和所有的交互作用的效应值;
- 识别重要的主效应和交互作用:帕累托图,或(半)正态概率图;
- 形成初始模型(全模型,包括所有主效应和交互作用)
- 进行统计检验——ANOVA方差分析
- 简化模型(移走不显著项,移走不重要项)
- 模型适合性检验:残差分析(正态性检验、残差与预测值的关系图等)
- 绘制显著且重要的主效应图、交互作用图;
- 解释结果
第一步,结果与从定义到实践:Design Expert完全析因试验(下)和从定义到实践:Shainin如何开展完全析因试验的计算结果完全相同。因为主效应和交互作用的计算,并不依赖于随机误差和方差分析。
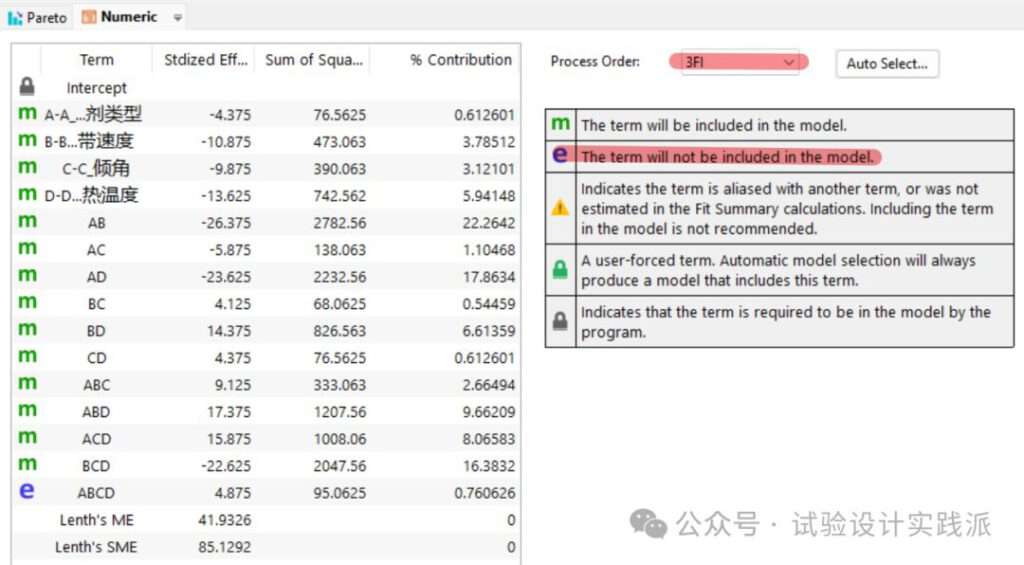
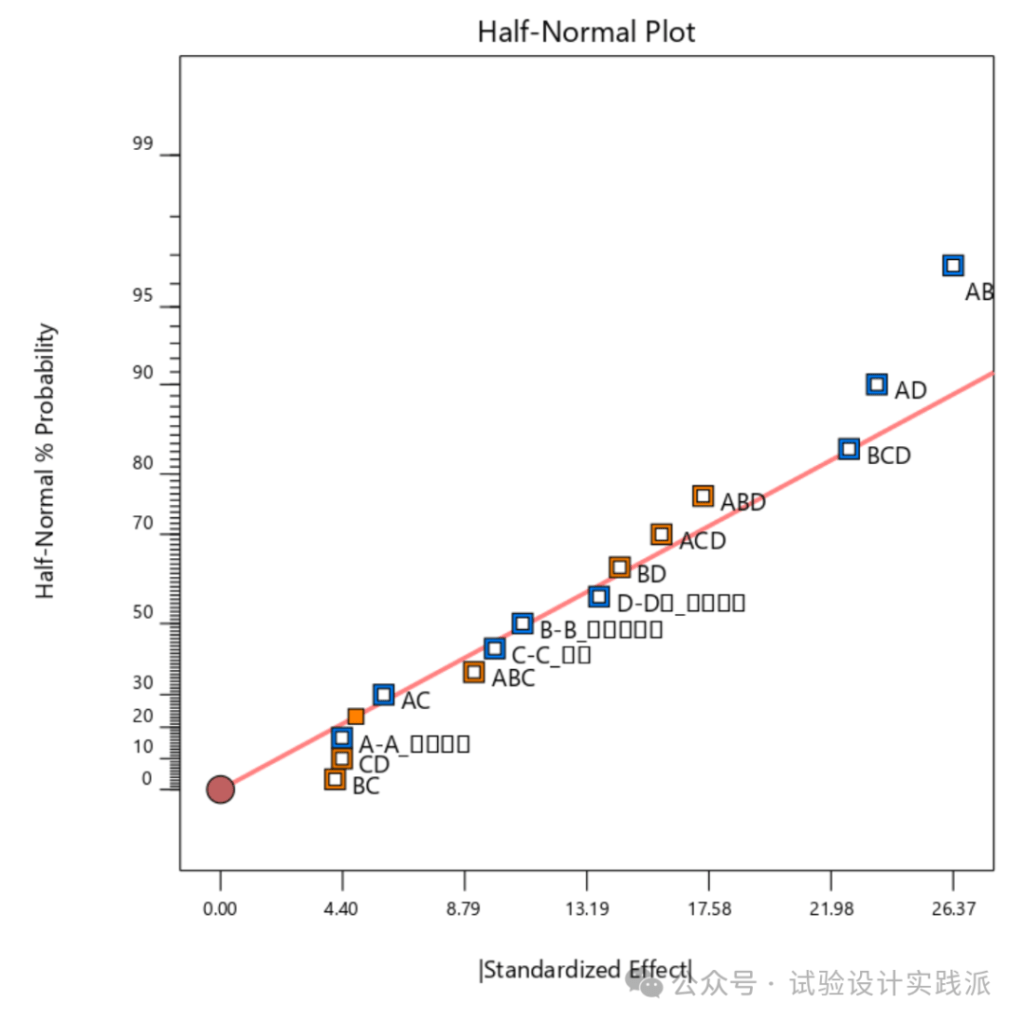
第二步,识别重要的主效应和交互作用,使用帕累托图和半正态概率图,是对第一步计算结果的排序和绘图;从两图看出,AB、AD和BCD是最重要的,BC、CD、A、ABCD是最不重要的。
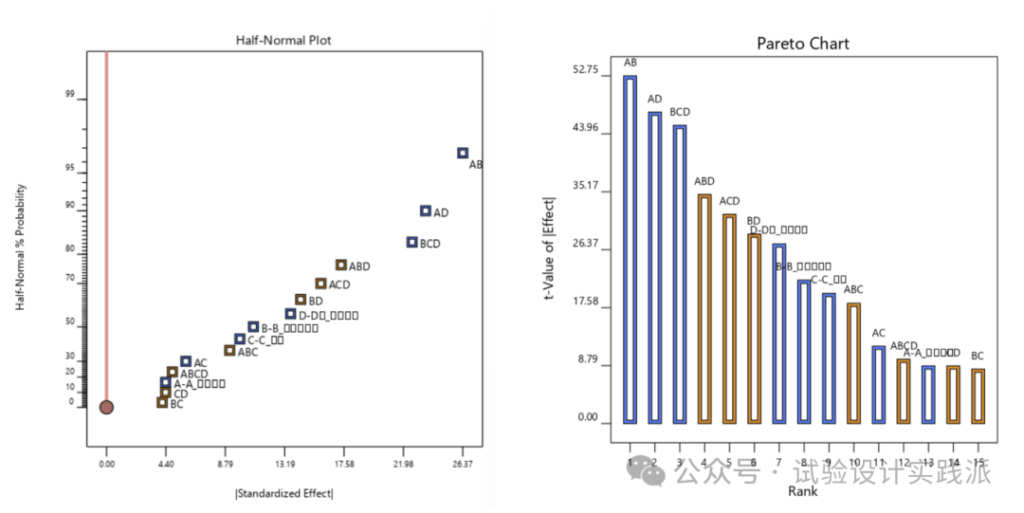
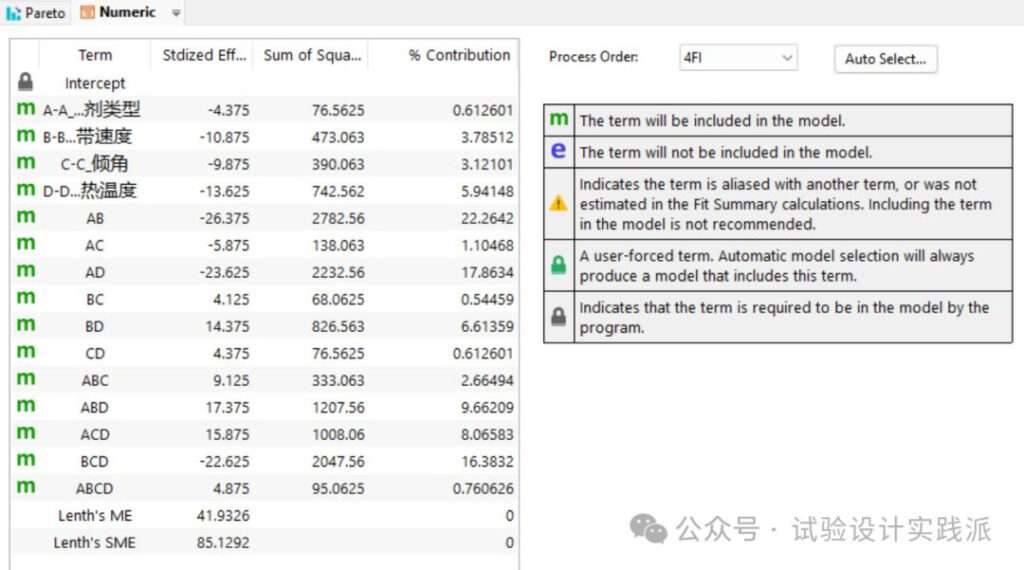
第三步,形成初始模型。
考虑所有的主效应和交互作用,根据效应值计算模型系数,得到Coded Equation。
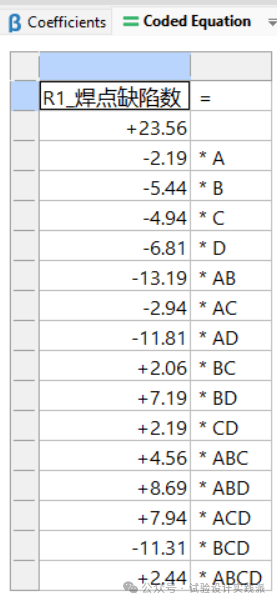
第四步,使用ANOVA方差分析识别显著的主效应和交互作用,这就出现问题了,如下图所示,主效应和交互作用的p值都为空。
因为纯误差项(pure error)的自由度从16变成0,所有的主效应和交互作用项都没有了比较的“基本度量单位”——重复的第一条重要性质。
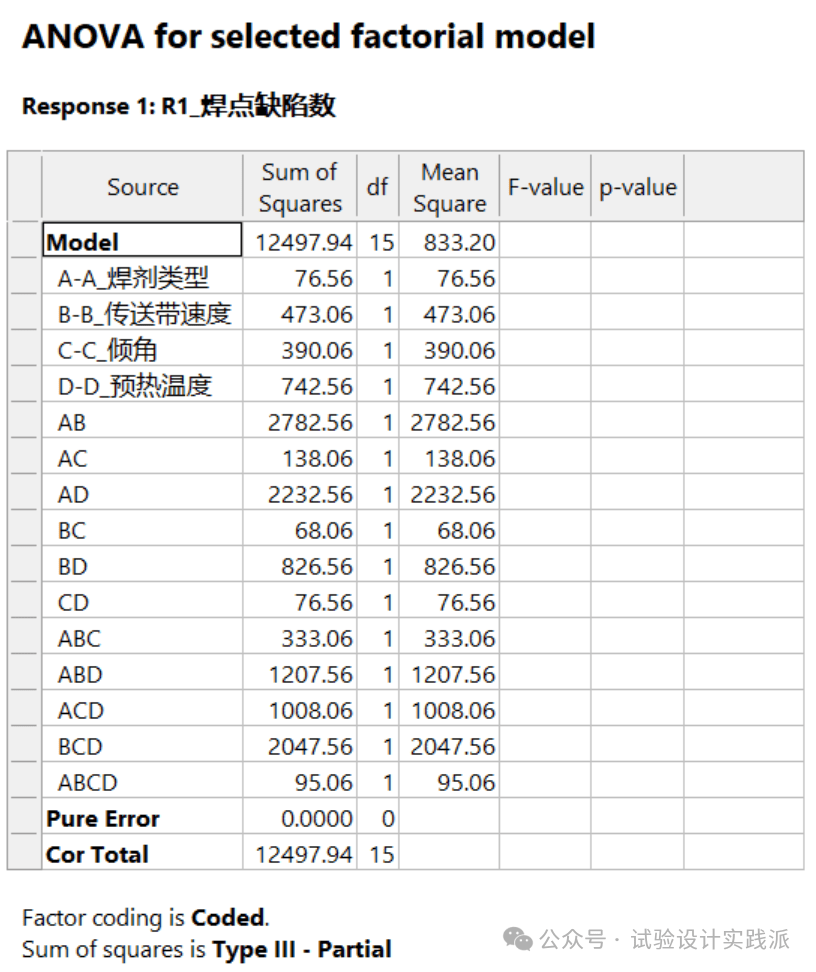
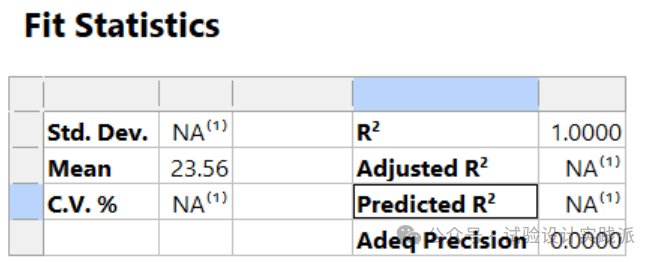
第五步,简化模型,无法“移走不显著项”,因为没有p值,不能判断哪些主效应和交互作用是不显著的。
第六步,模型适合性检验,目的是确定第四步方差分析结论是否可用。既然无法做第四步,那没有做第六步的意义。
Analysis –> Diagnostics –> Report
Diagnostic graphs cannot be created because the model is over-specified. All degrees of freedom are in the model and none are assigned to the residual (error). Notice also that the ANOVA had no calculated p-values because without residual error there is nothing to test against. To fix the problem, return to the Effects or Model button and assign at least one term to error.
第七、八步,绘制和解释显著且重要的交互作用,可以绘制却无法统计解释,因为没有重复试验,没法计算“置信区间”(confidence interval,CI)——重复的第二条重要意义。
无重复试验的改进策略
总结一下,无重复析因试验的核心问题是,没有重复试验,无法估算随机误差(纯误差),无法进行ANOVA方差分析,无法判断显著的主效应和交互作用,也就无法进一步简化模型。
有几个解决办法,核心都是随机误差的估算!
- 基于专业经验,回归到最简化的谢恩方法(Shainin,又译作谢宁),析因试验之前就明确测量系统的精度,放弃ANOVA方差分析和残差检验。
- 基于效应稀缺原理(sparsity of effects),将最高阶交互作用并入纯误差项,有了比较的“基本衡量单位”,就可以ANOVA方差分析。
- 如果无法判断是否显著,则将不重要的项并入纯误差,不重要的判断依据是第二步的帕累托图和半正态概率图。
- 部分重复,比如只重复几个处理组合;
- 中心点试验,重复2-4次,一方面验证随机误差,另一方面还可以验证模型是否存在弯曲。
- 如果知道随机变异主要来自测量系统,那就用“重复测量”替代“重复试验”;不到迫不得已不推荐,更好的办法是改进测量系统。
无重复析因试验的统计分析
回到摩托罗拉波焊案例,使用方法二和方法三简化模型,每移除一个交互作用,都要重新执行第二、三、四步,特别检查ANOVA方差分析的p值,以及模型拟合统计量;
- 移除四交互作用ABCD;
- 移除效应值
均方低且p值大的几项,比如:AC,BC,CD - 移除p最大的几项,比如ABC
所以首先删除四交互作用ABCD,如下所示
简化模型后,重新检视半正态概率图、帕累托图、ANOVA方差分析和模型拟合统计量,如下所示。
删除的四交互作用ABCD被移入纯误差(pure error),确定主效应和其他的交互作用的显著性。如下可见,都不显著(p>0.05),模型预测性很差。。。
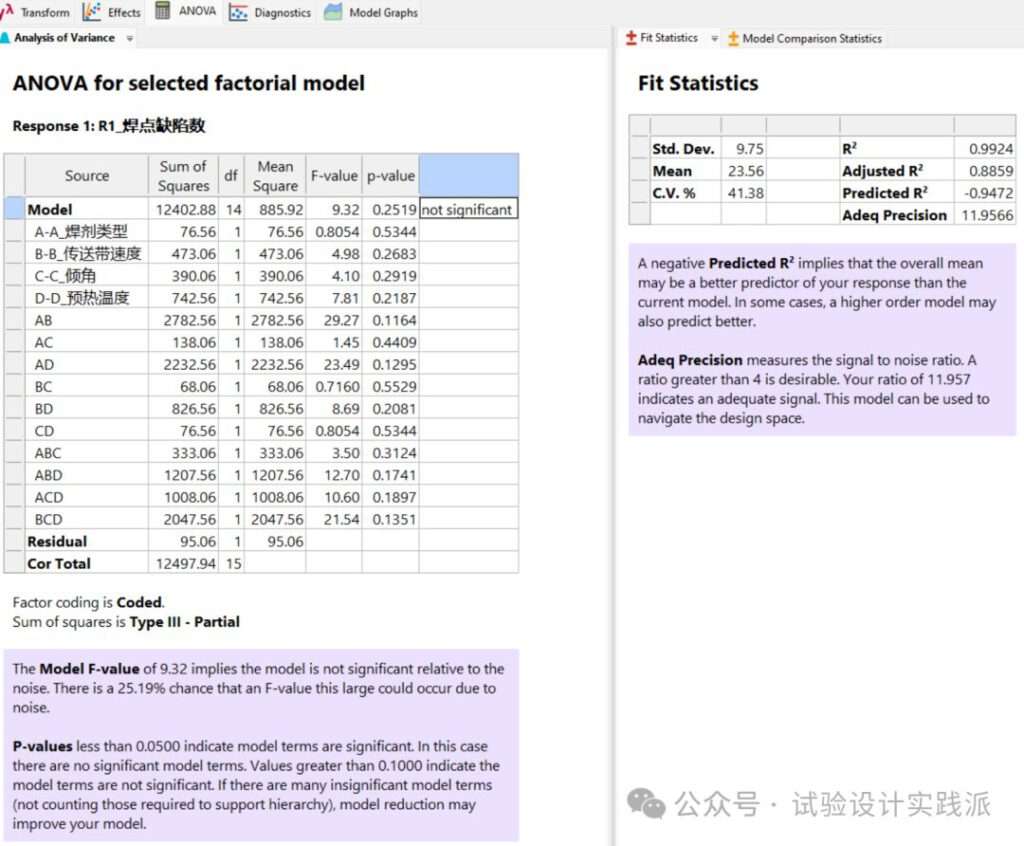
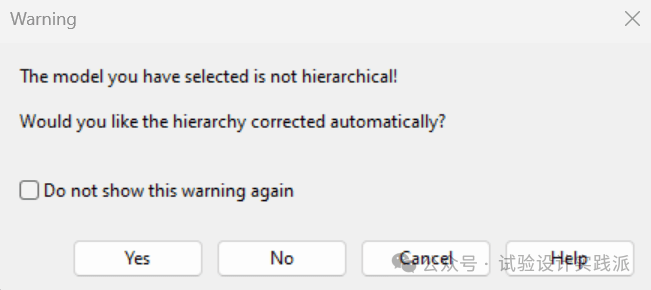
继续删除更多不显著且重要性较低(效应值均方较小)的交互作用项AC,BC,CD、ABC。重新执行ANOVA时,软件警告这样会违反“分层原理”(hierarchy principle);这个案例有些特殊,多个三交互作用比二交互作用更重要,保险的做法就是只能删除三交互和四交互,而不要移除二交互和主效应。
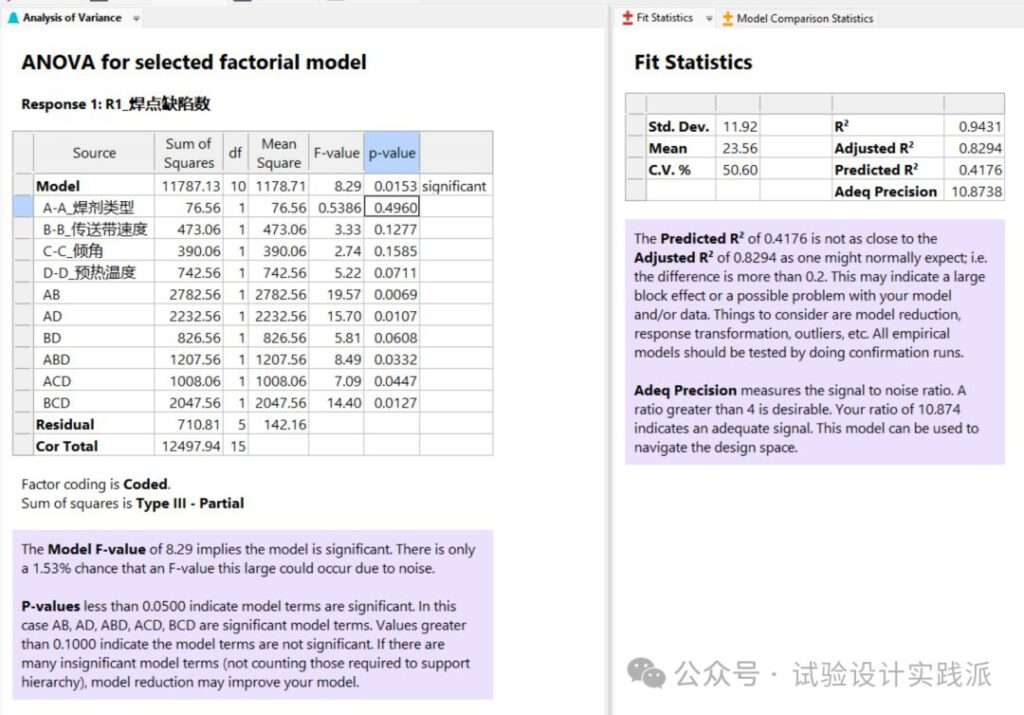
先不考虑分层原理,继续删除不重要的二交互作用,剩余二交互和三交互变得更显著,且模型预测性也有大幅改善。
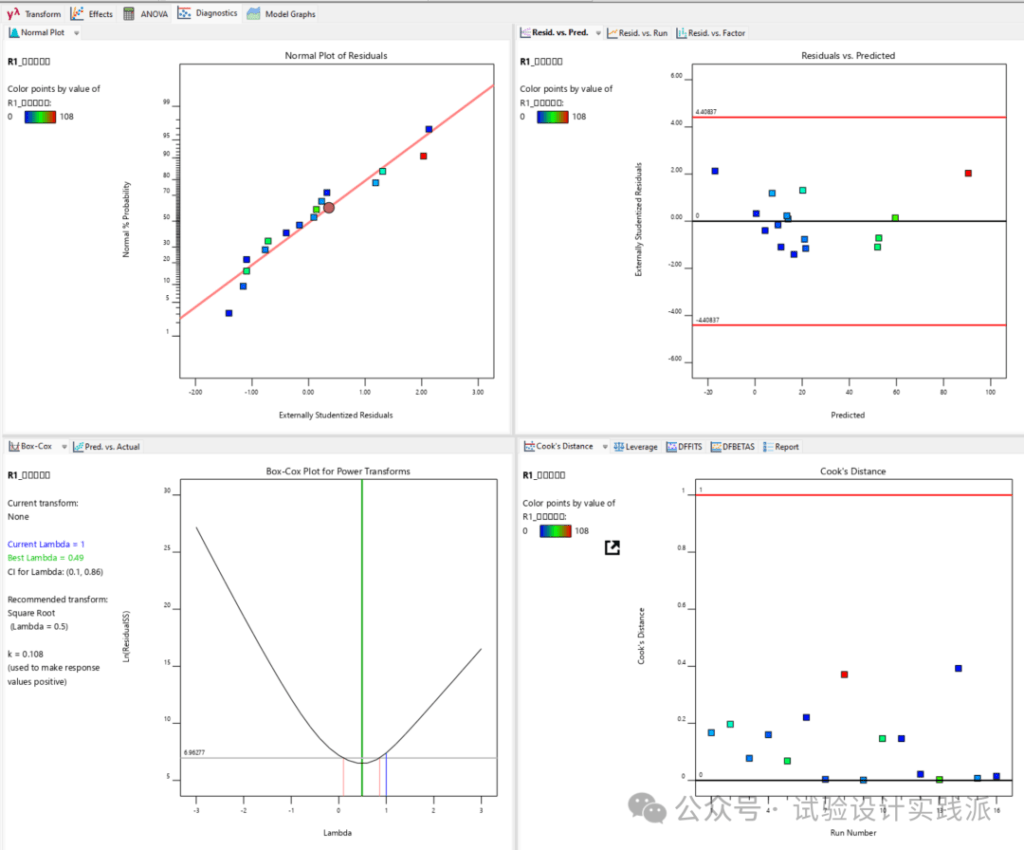
模型适合性检验如下,正态概率图和残差与预测值关系图还算正常;但是软件建议使用Square Root变换,变换后,模型拟合性有改善,predicted R^2为0.7,最重要的效应依然是AB、AD和BCD,并没有任何变化。更多响应变换的应用,未来再展开介绍。
绘制和解释显著的交互作用,最显著的是AB、AD和ABD。
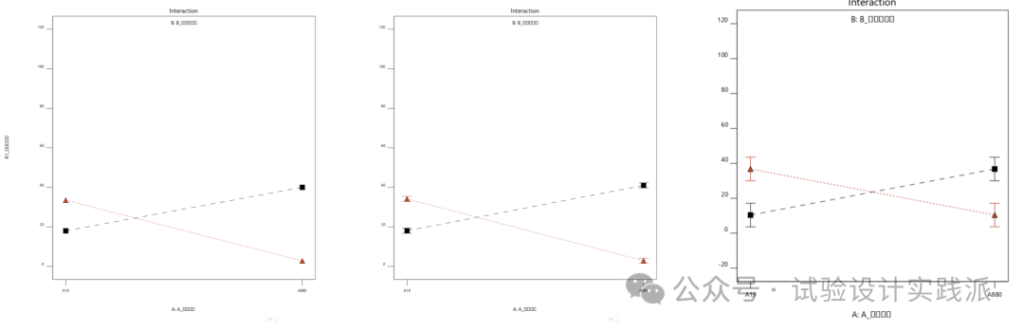
以AB为例,下图展示了无重复模型不简化、两次重复模型不简化、无重复模型简化后的二交互作用图,可见核心差异是置信区间。原因暂且不展开介绍,感兴趣者可以思考,未来介绍中心极限定理和置信区间时再展开解释。
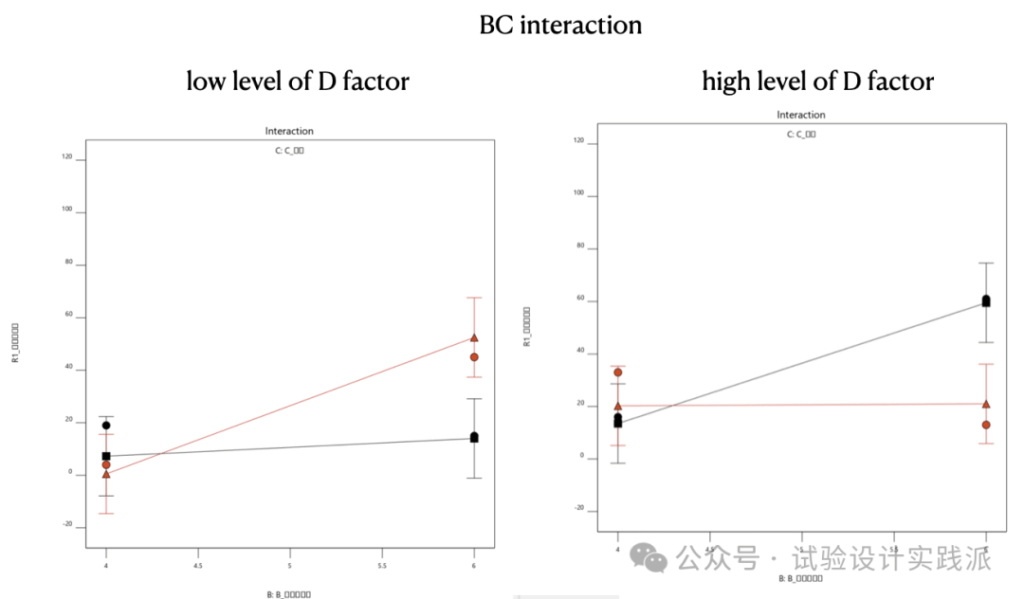
如下是显著的三交互作用BCD三交互,可见二交互作用BC在D的低水平和高水平是完全不同的规律,很有意思,需要结合专业知识解释背后的机理,这就是DoE带给试验者的专业知识,这就是DoE的价值所在。
本案例中的三交互作用是显著的,这也提示我们,要谨慎使用效应稀缺原理,如果是3因子2水平无重复完全析因试验,最好不要直接将三交互作用并入纯误差,而是老老实实做完全重复试验。
参考资料:
[1] 《试验设计与分析》
[4]从定义到实践:Design Expert完全析因试验(下)
✨ 欢迎关注公众号,一起学习和实践试验设计DoE。
✨ 如果本文对你有所启发,欢迎点赞👍、转发📣、推荐❤️、留言💬。
✨ 如果文章有任何错误,还望批评指正。
