在上一篇文章从定义到实践:Design Expert完全析因试验(下),我们基于摩托罗拉波焊案例,简单介绍了统计分析的步骤。相比从定义到实践:Shainin如何开展完全析因试验的手动筛选红X,统计分析引入了更严谨的统计工具:ANOVA、模型检验、残差检验等。
然而在实践中,即使“严格按照软件流程”进行统计分析和推断,仍会遇到一些困惑:交互作用全显著、删项出警告、LoF变显著、模型建议转换……
本文尝试解释摩托罗拉波焊案例中的第一个“看起来不合理”的现象,如有解释不清甚至错误的内容,还请大家批评指正。
❓摩托罗拉波焊案例中,为什么所有交互作用都显著?
如下图所示,ANOVA方差分析显示所有的主效应、二交互作用、三交互作用,甚至四交互作用,都是非常显著的,即p<0.01。
模型的p值也<0.01,只有不到0.01%的概率,模型因为噪声(随机性变异)而如此显著。(there is only a 0.01% chance that an F-value this large could occur due to noise.)
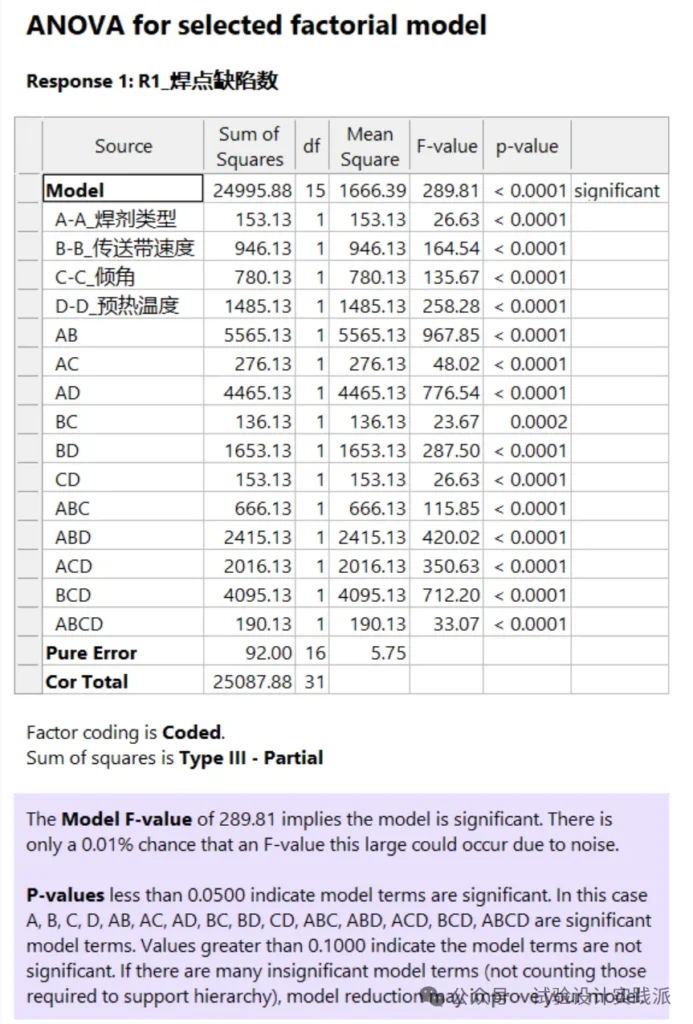
结果看起来还算正常吧?
但是,根据“效应稀缺原理”(sparsity of effects,三交互及以上高阶交互作用,在现实中很少存在),结果看起来又不太正常?
答案隐藏在ANOVA方差分析的纯误差(pure error)中。纯误差代表的是试验中不受控制的随机变异。
简单的量化纯误差的办法是重复试验,这也对应DoE三大原则的重复(replication)。
基于所有同一试验组合的两次重复试验结果的差异,计算出纯误差的方差、均方。
上图可以看出,纯误差的自由度达到16(足够多的重复试验),纯误差的均方只有5.75,只有主效应和交互作用的均方的1/10甚至1/100,所以主效应和交互作用都显著。
我们可以仔细查看下图的原始数据,了解重复试验的波动情况。
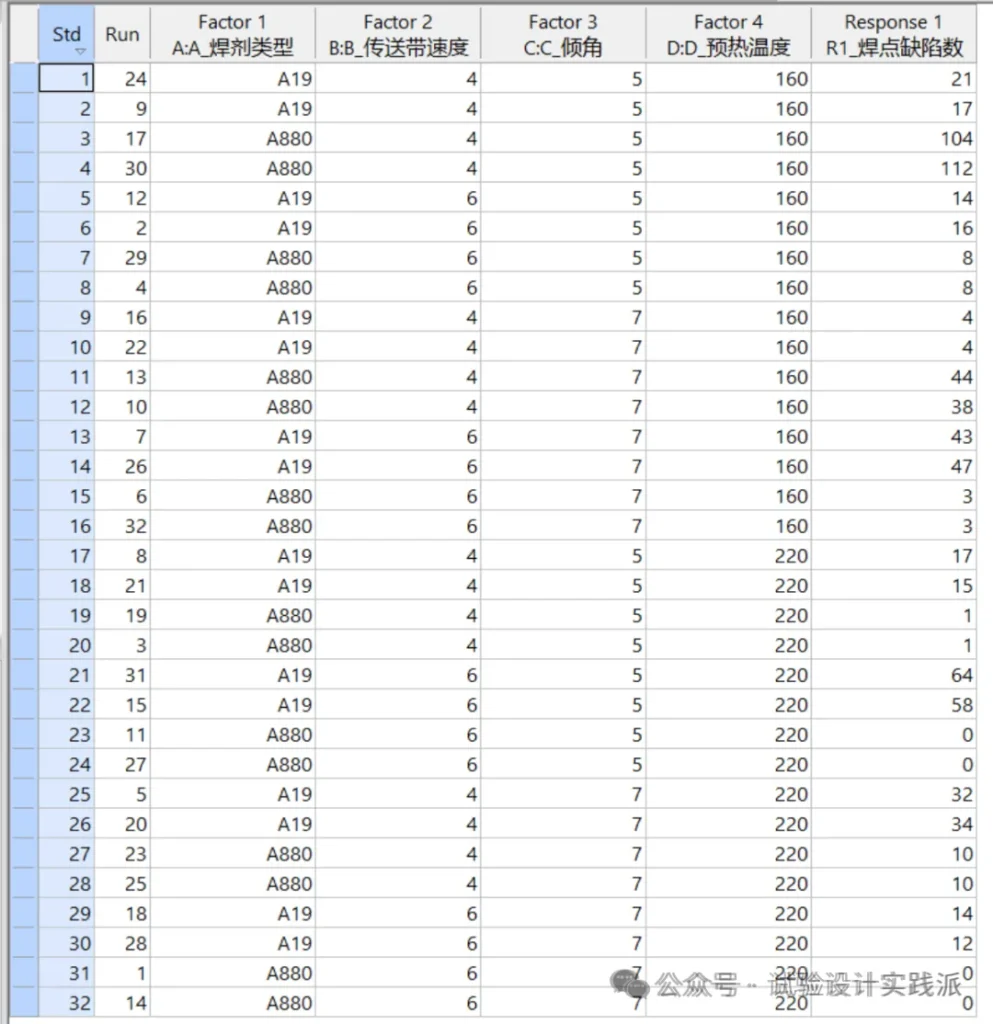
从上图可以发现,试验重复性都很好。对于每个试验组合,最大组内差异是8(std 3和4,此时缺陷数>100);其次是6,5,4,2;最小的组内差异是0,更重要的是,对于所有缺陷数<10 的试验组合,组内编变异都是0!
虽然使用随机化“平均掉”可能存在的、未纳入试验的影响因素,进而将其影响合并到”纯误差”(pure error)中(试验设计DoE的三大原则:随机化、区组化、重复),但每个试验组合的重复性都很高,这充分说明整个试验的随机变异很小。
反映在ANOVA方差分析上,就是每个主效应和交互作用的均方都很大,纯误差(pure error)的均方很小。
“多大是大,多小是小”?就看两者的比值——即F值,及其在F曲线(类似于下图)上对应的概率——即p值!
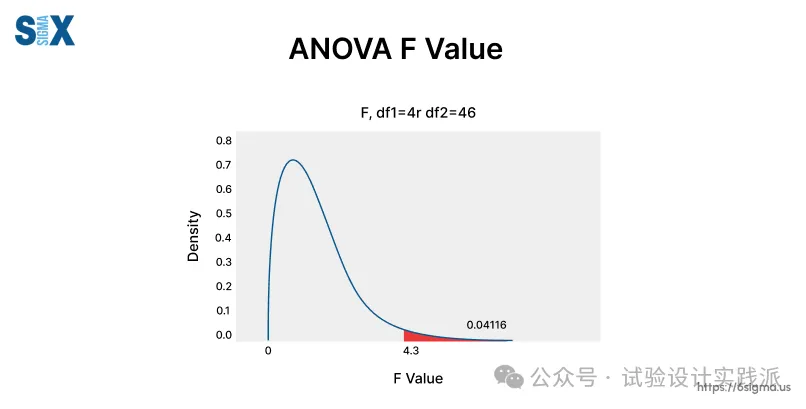
这就是ANOVA方差分析,即F检验,通过比较效应和纯误差的变异,判断相对于纯误差,效应是否显著。
The F-test compares the variance among the treatment means versus the variance of individuals within the specific treatments. High values of F indicate that one (or more) of the means differs from another. 《DoE Simplified》
再回头看问题,答案就很自然了:所有的交互作用都显著,很正常。因为试验控制得好,“不可控因子”很少,以至于所有的”控制因子“及其交互作用都能被精确量化。
但是,所有的交互作用显著,并不代表都重要,并不都值得展开研究。
正确做法是,考虑显著与否的同时,对主效应和交互作用的效应值进行大小排序,方法有很多:
- Shainin方法:手动排序效应值,选择前三名:红X,粉红X,浅粉红X
- 使用方差分析表,查看F-value或均方(Mean square),选择前几名;
- 使用帕累托图(Pareto Chart),选择前几名;
- 使用“半正态概率图”(half normal plot),选择最右侧的几个效应。
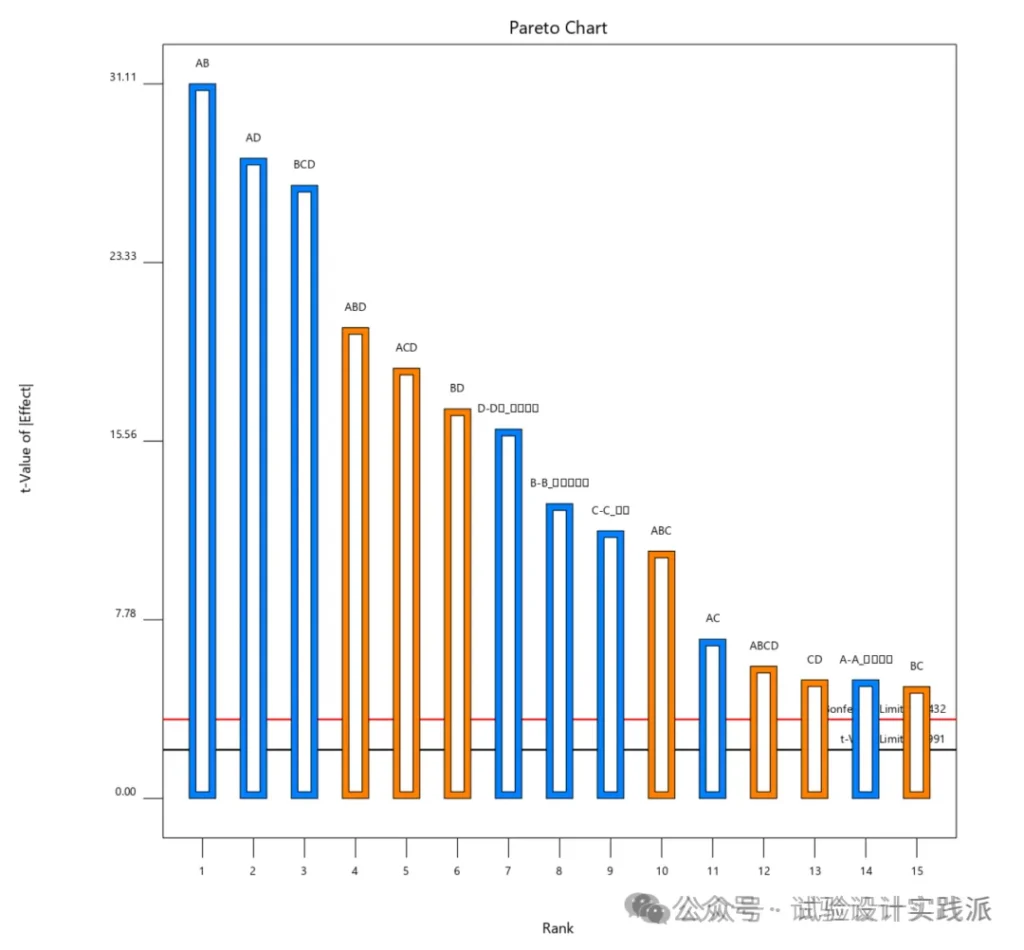
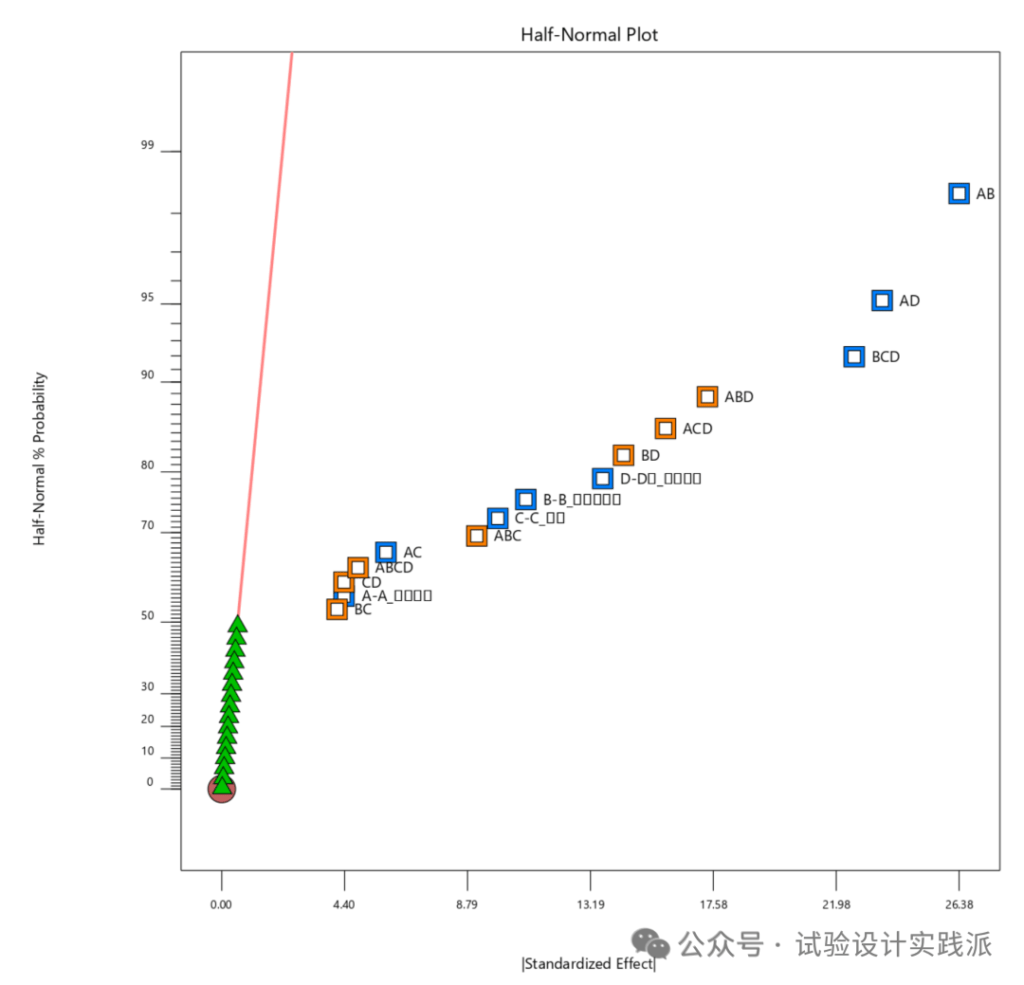
📌 综合而言,既要看p值,又要看效应值的相对大小。前者是与纯误差(随机变异)比较,后者是与其他的效应比较。
Shainin方法强调“效应大小排序 + 实际验证”,而DoE软件提供了“方差分析ANOVA”结果以辅助判断。两者也并不冲突,而是相辅相成。
