本文简单总结蓝皮书第四章“统计基础” – 4.1 正态总体的抽样分布知识,只列重点,梳理我的思考,细节内容还要翻书。参数估计(点,区间)单独再总结一篇文章。
之前已经整理了第五章假设检验(1234部分)、第11章测量系统分析、第12章SPC这几部分的内容。
2022-7-21 今天重读蓝皮书,刚想明白了下面两个问题和书中的一个图,如下,想通了感觉好简单(但是这本来就是非常基础的知识点啊)。
问题:一个总体分布,均值u,标准差𝛅,为什么抽样n次得到的样本,标准差=𝛅/(sqrt(n))(sqrt是开根号)。为什么样本标准差反而变小了,得到的样本分布比总体分布更瘦了?
答案:如果一个总体分布是一万名学生的身高,那随机抽取一万名(取完放回),样本分布和原来的总体分布重叠吗? 注意抽样是取出又放回,而且总体均值的学生数量是最多的。所以抽取一万名学生,并不是把总体挨着抽了一遍,最高和最矮的学生说不定一次没抽到呢(计算一下概率,低于万里挑一?)。这样就明白了怎样“通过抽样推测总体的情况”,特别是根据样本标准差计算总体的标准差;有了总体分布,然后就很容易知道怎样“分析样本时候属于某个总体”,
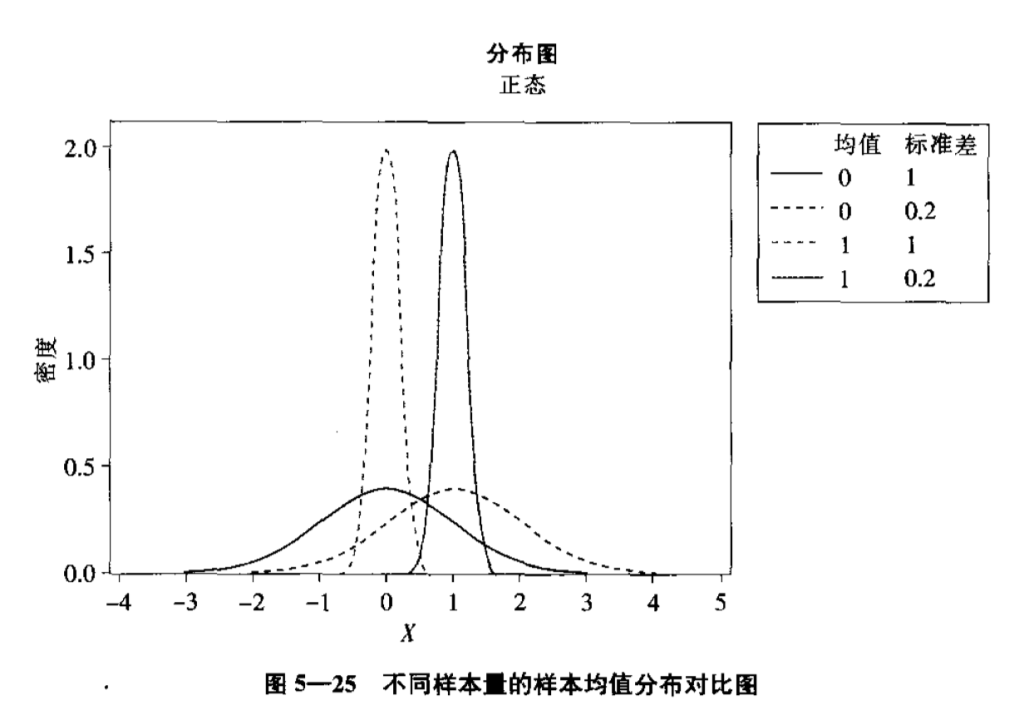
问题2: 下图的两个矮胖的总体分布,如何确定一个样本属于哪个分布?
答案:只抽样一次,肯定无法区分。通过多次抽样(抽样次数多少正好?正好的定义是什么),抽样分布变窄变高,两个总体分布对应的n次抽样分布能分开(怎样定义),就可以判断样本属于哪个总体了。
4.1.1 样本均值的分布——标准正态分布及t分布
统计的基础是抽样,通过抽样去“推测”总体的情况,分析样本是否属于某个总体,等。
抽样分布是一种“可视化的描述方式”,分布曲线可以告诉我们位置(center)和波动(spread,胖瘦),center和spread也是最基本的统计数字。
抽样分布对应分布曲线,曲线都有参数,通过比较参数,判断分布之间是否相同。
1. 分布曲线:抽样分布,正态分布,准正态分布,t分布
抽样分布:从总体中抽样一次,得到的分布曲线。(这么说其实是不对的,一次抽样不能推导出分布曲线。之前写这句话肯定没理解清楚P184的这句话:“如果只抽取一个样本,这时它本身就是样本均值,样本均值的分布与原来总体的分布完全一样”。
对于正态总体的统计量进行抽样分析,反复抽样n次,得到一组样本(n个数据),分析该样本的统计量比如“均值“·,其分布服从正态分布还是t分布。【这里面有一个概率问题,即一次抽样的结果,可能和总体分布相近,也可能偏的比较大,就像分析收入分布,如果抽到比尔盖茨,那就偏差太大了】(2022-7-21 这儿之前又理解错了)
“正态总体”是抽样分布的前提,如果总体本身不是正态分布,那就研究抽样分布就没有意义了。如果不能确定总体的情况,就应该进行“正态检验”!
抽样分布:从一个总体中,反复抽取一定数量的抽样量,所对应的分布。比如从南开大学随机找100名大一新生,做一个简单的生活费调查。总体是所有的新生,统计量是每月生活费,抽样量是100。再比如研究膨润土活化添加量对铸造GCS性能的影响,一个样品,分成三份样品,各测量一遍GCS。这儿总体是”某活化添加量对应的膨润土样品“,统计量是GCS强度,抽样量是3。
当然要绘制这个分布曲线,就需要”反复抽样”,但是分析一次抽样的统计量数据,则一次抽样。
抽样量——抽样量是抽样分布的关键变量
这儿的关键问题就是“抽样量“,抽样样本的波动和样本量关系密切!这也对应于《思考,快与慢》中所说的”大数定理“和”小数定理“的含义,抽样量大(大数)得到的分布更接近真实情况,不容易出现异常统计量;如果只抽取几个样本,很容易得到极端的数据。
只要抽样量不要太少(具体是多少,答案是中心极限定理),我们通过抽样得到的都是“准正态分布”,就可以直接用正态分布的规律。
但“抽样量不足”时,抽样分布就不应该直接用正态分布,而是应该用t分布(student分布),如果用正态分布就会有比较大的误差,因为抽样量不足时,t分布更“胖”,不符合正态分布的“68-95-99.7规律”。当抽样量足够高时,t分布就和正态分布(Z分布)一样了。
多少的抽样量算“不足”? 经验看,自由度超过30以后,二者差异很小,此时完全可以用标准分布替代t分布。
如何定量判断合适的抽样量? 答案是“统计检验功效”,具体见“5.8样本量的计算” 《六西格玛管理统计指南》第五章假设检验-4 样本量和统计功效
正态分布和t分布的区别是:前者与抽样量无关,因为正态分布是一种“理想的、抽样量够大,且通过重复抽样”得到分布曲线,默认抽样量是足够大的。 实际抽样量当然是有限的。(正态)
但是只要达到一定的数量(具体是多少),分布曲线与正态分布曲线的重叠程度足够高(如何定量衡量),那就直接用正态分布曲线解决问题即可。
t分布(Student 分布)
而t分布是与抽样量有关的曲线,所以不仅一条,随着抽样量n的增加,t分布曲线逐渐趋近于正态分布曲线。
2. 何时用t分布?
答案:抽样量比较少的情况,比如只做了五次重复测试,甚至只有可怜的两三次。
具体而言,可以看“正态性检验”
3. 正态性检验
许多统计问题的解决依赖于数据服从正态分布,因为我们必须先判定数据是否服从正态分布。P114
4. 我们什么时候还会用到分布曲线?
4.1.2 双样本均值差的分布
“均值差”的分布,不是均值分布的差;对于前者,这其实还是一个单样本的均值和标准差的计算,很简单。
4.1.3 正态样本方差s^2的分布——卡方分布
比较样本之间的均值,直接加减即可,当然要说谁大谁小,还要借助标准差,进行严格的假设检验。
而要比较样本之间的标准差,千万不要直接标准差加减,这里需要用卡方检验chi-squre。
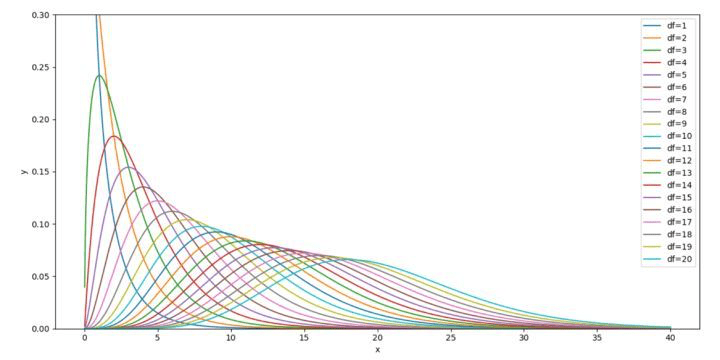
卡方分布是从正态分布中随机选出n个样本,其方差的分布情况。(重复抽样,得到分布;不是只抽一次)。
n越大(抽样量),卡方分布越向右倾斜。
我们知道标准正态分布的分布曲线,也知道它的卡方分布。
然后我们就可以比较分布曲线之间是否相同,“胖瘦”对比,利用的就是卡方分布。
拟合优度检验,同样是比较分布之间的相似性。
4.1.4 两个独立的正态样本方差之比——F分布
卡方分布只是分布曲线,两种分布之间的对比,使用的是F分布。
用途:判断两个正态总体方差是否相等(方差比较),多个样本之间的方差比较(ANOVA分析)。
标准差以内的百分比,更精确的数字是68.27%、95.45%及99.73%。
1. 参数的点估计
2. 参数的区间估计
Note:
2020.9.16 重新思考“分布曲线”第一部分
2020.9.29 简单更新
2022.7.21 更新第一部分
2022.8.23 简单更新第一部分发布,点估计和参数估计以后单独整理发布。