本文基于《世界级质量管理工具》案例,分享谢恩(Shainin,又译作谢宁)DoE如何进行完全析因试验
在谢恩DOE中,经过“一线工人告诉你哪些是重要的因子”的线索生成试验以后,全部析因或变量搜索可在一次析因分析中干净利落地分离主因子、二阶及更高阶的交互影响,并可以进行量化。
完全析因试验是所有正规的试验设计中的最佳技术,因为全析因可以简捷而又正确地识别和量化每一个一阶影响、二阶影响、三阶影响及四阶交互影响效应。实际上,试验设计的研究先驱和鼻祖Fisher爵士仅使用全析因而没有借助于计算机。他决不利用部分析因之类的捷径来玷污他的成果。《世界级质量管理工具》
案例介绍:摩托罗拉波焊
15 年前,一个指导工作小组承担了波焊工艺的改进工作,该小组的成员仅参加过一次作者关于试验设计的讲习班。当时的可焊性缺陷水平高达10000ppm。该小组雄心勃勃,其目标是将缺陷水平降低到200ppm以下,即改进高达50:1,实际上,在20世纪80年代早期,世界上还没有一个波焊工艺的缺陷水平能低于10000ppm~15000ppm。
该小组决定进行具有4个因子、每个因子2个水平的全析因试验,具体如下:
| 因子代码 | 因子描述 | 因子水平 (-1) | 因子水平 (+1) |
|---|---|---|---|
| A | 焊剂类型 | A19 | A880 |
| B | 传送带速度 (英尺/分) | 4 | 6 |
| C | 倾角 | 5° | 7° |
| D | 预热温度 (°F) | 160 | 220 |
1. 如何试验
4因子2水平总共16次试验,按照随机表排列后,逐一试验。
再次随机排列16次试验,逐一试验,完成第二次完全重复。
取两次试验结果的计算值,作为每个组合的响应值。 注意是两次随机重复试验,不是重复测试。
若每一部件的两个读数相差太大(例如,超出±10%的范围),则表明该试验的“噪声”太大。可能需要选择其他因子或水平或者需要通过过程确认,使这些不可控制的(噪声)因子更加受控。p303
水平的选择建议:水平-1为当前的工艺条件,水平+1为“假定会产生更好结果”的工艺条件。
试验结果整理在如下的全析因矩阵中,矩阵右侧和下侧的各四组数据,分别是每行和每列的四个试验组合结果之和,比如150为第一行的试验之和,即因子D为-1水平和C为-1水平时的四次试验之和。
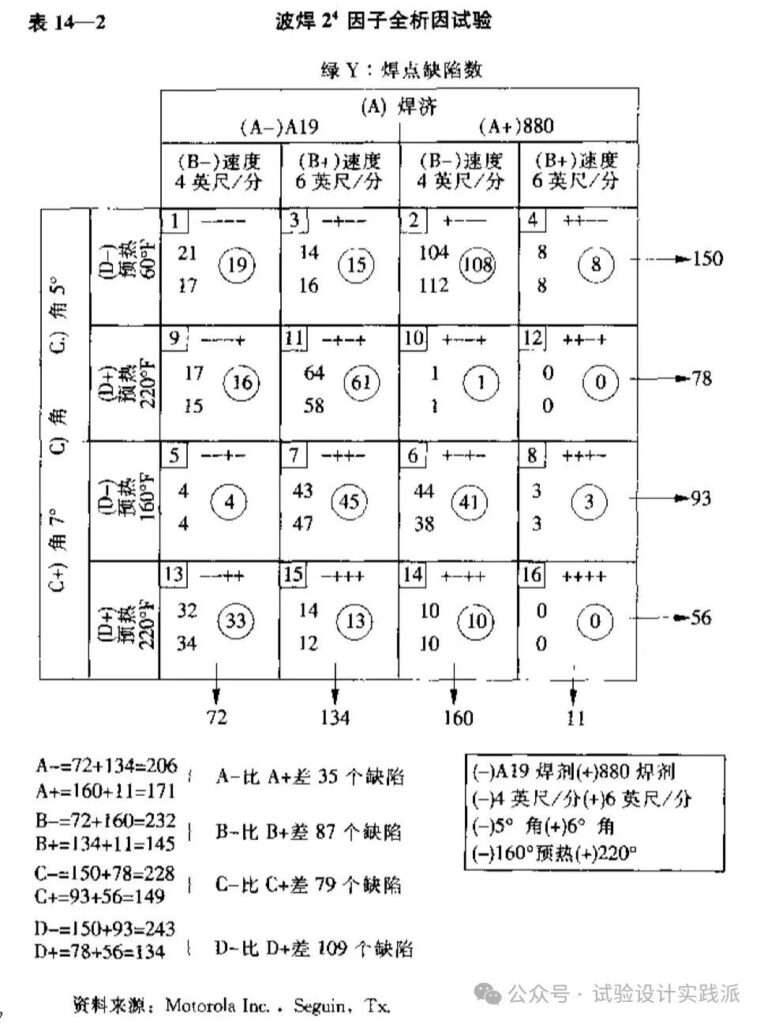
2. 方差分析(ANOVA)
第一步,构造如下的方差分析(ANOVA)表,一共16次试验组合,最右一列数据是每个试验组合的响应变量,即两次试验的平均值。
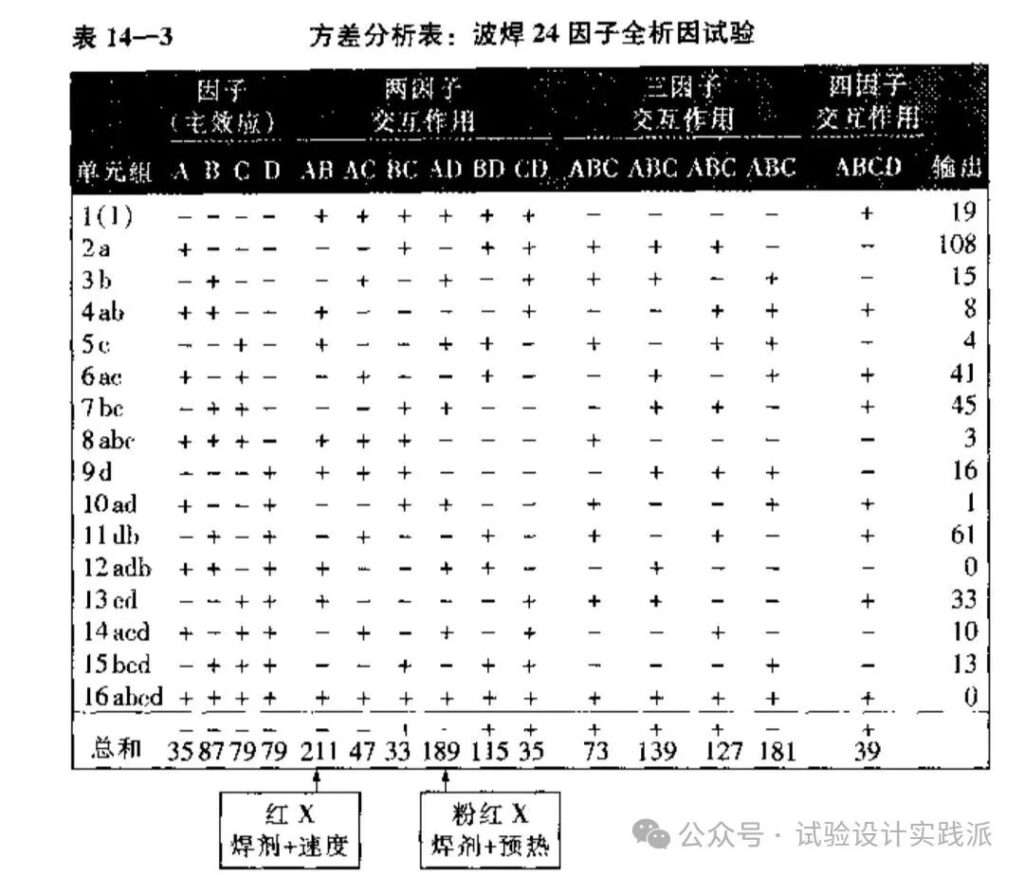
值得注意的是,根据A、B、C、D的水平组合(前四列),可以推出二交互、三交互、四交互的水平,即第5列AB到第15列ABCD的水平。
方差分析表一共包含16个试验组合和15个研究变量,正好也是正交表L16(2^15)。 换言之,如果从正交表出发设计完全析因试验,殊途同归,也会得到这样的方差分析表。但是要注意如何分配这15个变量。
L16(2^15)正交表:
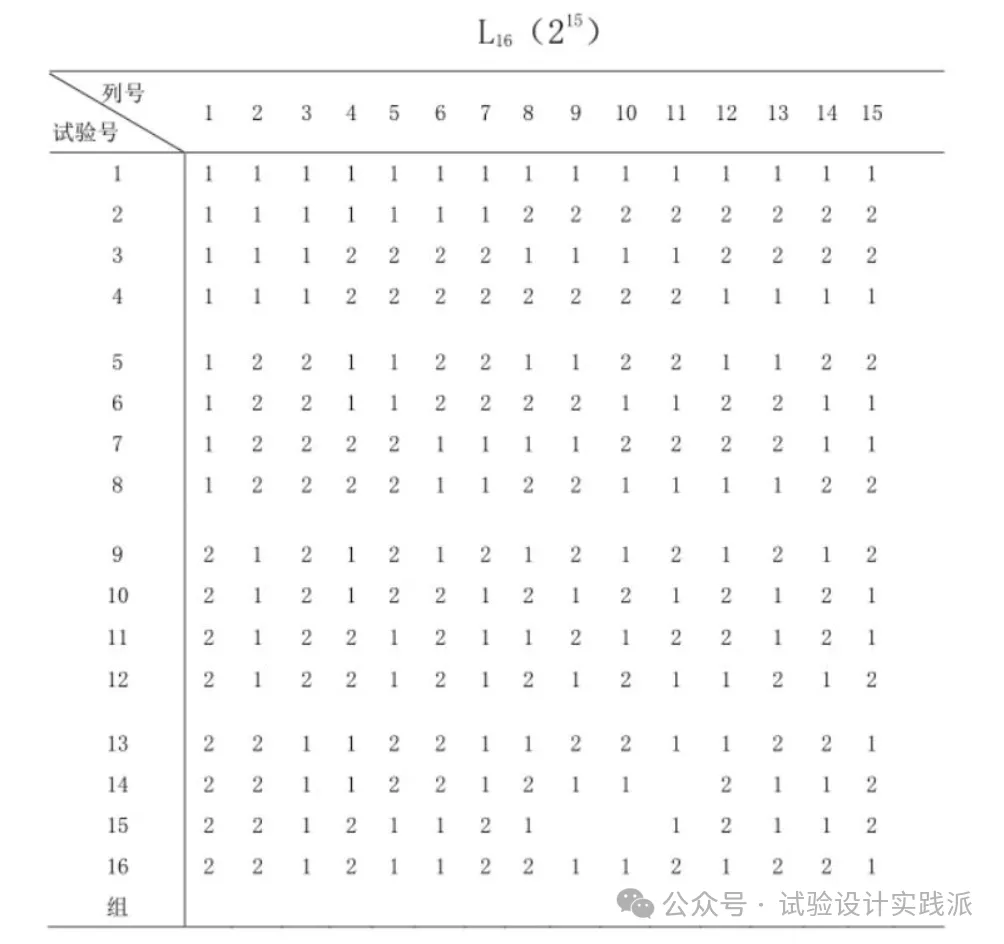
第二步,(手动)计算主效应和交互作用的大小,置于最后一行”总和”。
表14-2给出了四个因子主效应的计算过程,如下是计算原理,该计算原理同样适用于交互作用。这样计算交互作用,比基于交互作用原理(见DoE基本术语)的计算方法要简便,后者并不适合手动计算,特别是三交互和四交互作用。
对于32组读数,将每个部件中A为(-)的平均部件读数相加,并将每个部件中A为(+)的平均部件读数相加。因为所有其他因素(B、C和D)都是相互平衡的,也就是说,它们对两个水平都加上或减去了一个常数,因而没有改变它们的初始差别,所以说,A(-)和A(+)之间的差别是由因子A引起的与此类似,将每个单元中B为(-)的平均部件读数相加,并将每个部件中B为(+)的平均部件读数相加。它们的差别是由因子B引起的。用类似的方法可得到C(-)和C(+)、D(-)和D(+)平均数之间的差别。 p303
备注:方差分析表14-3充分体现了谢恩DoE的魅力,既能快速理解主效应和交互作用的计算原理,又能直观排列识别显著因子!
第三步,按照从大到小排序,可以识别出红X、粉红X、浅粉红X。
方差分析表14—3最后一行”总和”,以准确的量化形式给出了每一个因子以及两交互、三交互和四交互作用的大小和影响方向(+或-)。在这4个主效应及11个交互作用中,最显著的变量依次是两因子AB交互作用(红X)、两因子AD交互作用(粉红X)和三因子BCD交互作用(浅粉红X)。
所有的主效应都不如二交互作用AB、AD和三交互作用BCD显著!——这就是一次一因子试验(OFAT)无法给出的结论,也充分体现了试验设计DoE的核心优势——识别和量化交互作用!(具体见:从爱迪生到DoE:告别蛮力试验)
第四步,可视化,绘制交互影响效应图
从下图可以看到每个因子的主效应,直观查看二交互作用——交叉代表显著的交互作用。 (备注:下图的BCD交互作用有误,暂忽略)

3.确认试验:求交运算
谢恩DoE中完全析因试验的确认试验,是将上一步筛选出来的显著因子和交互作用,合并在一起,设定为最佳水平,做出”最佳样品”,确认改进效果。
使A,B,C和D保持其(+)水平,在17块新型电路板上进行求交运算。每块电路板上有800处连接,其缺陷率降低至220ppm,尽管没有完全达到该小组的目标(即50:1的改进),却也取得了45:1的改进。在20世纪80年代早期,无论在美国还是在欧洲和日本,都没有人在波焊工艺上达到如此低的缺陷水平。
该小组继续对该工厂的其他12台波焊机进行类似的参数修改。他们减少了20名修理员及相同数量的质检员,每年节省开支75万美元。该小组的组长在工作中逐步迷上了试验设计,每周都主动进行1至2次试验设计。他原来是一名维修技师,后来晋升为拥有1800名员工的得克萨斯工厂的首席试验员和督导。
这一步是微缩版的谢恩DoE验证工具——”B vs C”,C(current)代表当前的产品,B(Better)代表更好的产品。
确认改进的程度及持久性的最佳方法是:回到改进前的产品、工艺或方法,并确保问题再现。然后,转用新改进的产品、工艺或方法,并确保问题“归零”。至少重复两次上述过程。这就像打开电灯的开关一样,复现问题,问题“归零”;再复现问题,问题再“归零”。只有这样,试验人员才能得到关于改进持久性的足够的置信水平。《世界级质量管理工具》
学习谢恩DoE的一点感触
谢恩DoE或谢恩解决问题框架的优势之一是学习难度低。作者认为技术人员和一线工人只需要1天培训就可以上手实践。
我认为,完全析因试验就能体现这一点,上手快,不用试验设计软件,通过绘制全析因矩阵、方差分析表、交互作用图,手动计算出所有的主效应和交互作用,筛选出红X、粉红X、浅粉红X。
没有试验设计软件中的残差分析、正态性检验、模型检验等,看起来简陋又不够严谨,但多数情况够用了,我认为有几个原因:
1. 通过重复试验判定误差大小,代替更繁琐的残差分析和显著性检验
2.前期的线索生成工具和变量搜索,可以大幅降低完全析因试验出现异常的概率。
3. 最重要的是,用结果说话,用“B vs C”验证试验确认新工艺参数的试验效果。
✨ 欢迎关注公众号,一起学习和实践试验设计DoE。
✨ 如果本文对你有所启发,欢迎收藏、点赞、转发。
顺祝大家端午节快乐
