Design Expert响应变换：摩托罗拉波焊案例的延伸思考和操作指南

导语：在析因试验分析中，残差检验常提示模型假设不成立。响应变换（transformation）是改善模型拟合、简化模型、提升预测精度的利器。本文以摩托罗拉波焊案例为背景，详解如何利用Design Expert便捷地进行响应变换，并对比变换前后的显著效果。
本文继续围绕《世界级质量管理工具》中的摩托罗拉波焊案例，介绍析因试验（Factorail design）的统计分析方法；先简单回顾基于这个案例的已发布文章：
问题回顾与残差检验
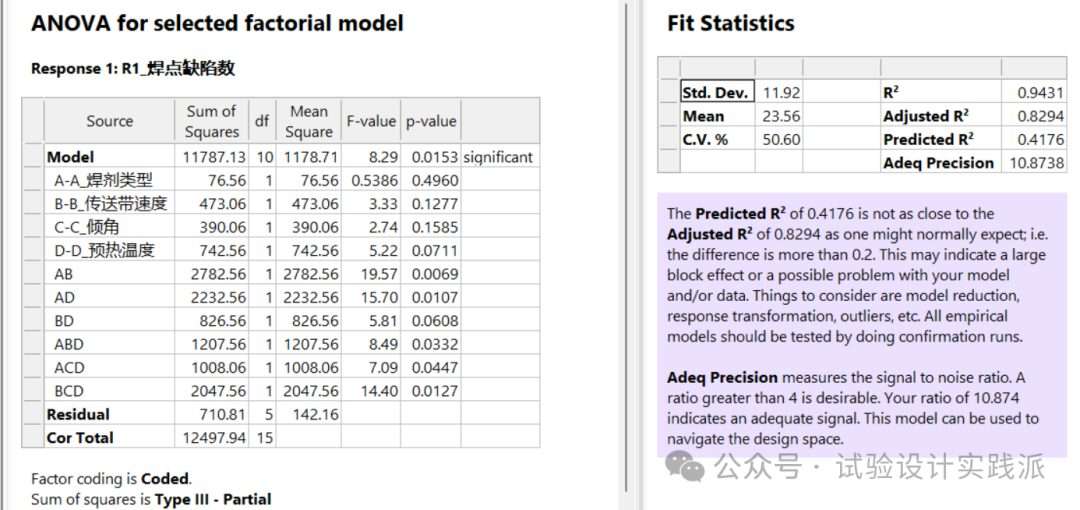
在无重复析因试验中，基于效应显著性及工程重要性进行模型简化，ANOVA方差分析结果如下所示。
图片
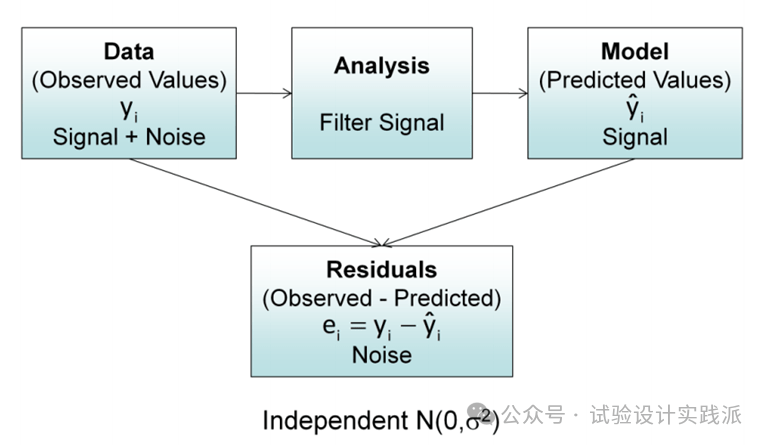
ANOVA分析的核心假设之一是：残差(Residuals，即观测值与模型预测值之差) 应服从正态独立分布，且与预测值(Pred.)、运行顺序(Run)、各因子(Factors)等变量均无关。如下图所示：
图片

在实际当中，这些假定条件通常不完全成立。因此，在这些假定条件的有效性尚未核实之前就依靠方差分析，通常是不明智的。是否违背了这些基本假定和模型的适合性，可以很容易地利用残差检验来进行分析。

《实验设计与分析》
残差检验的结论如下图所示：
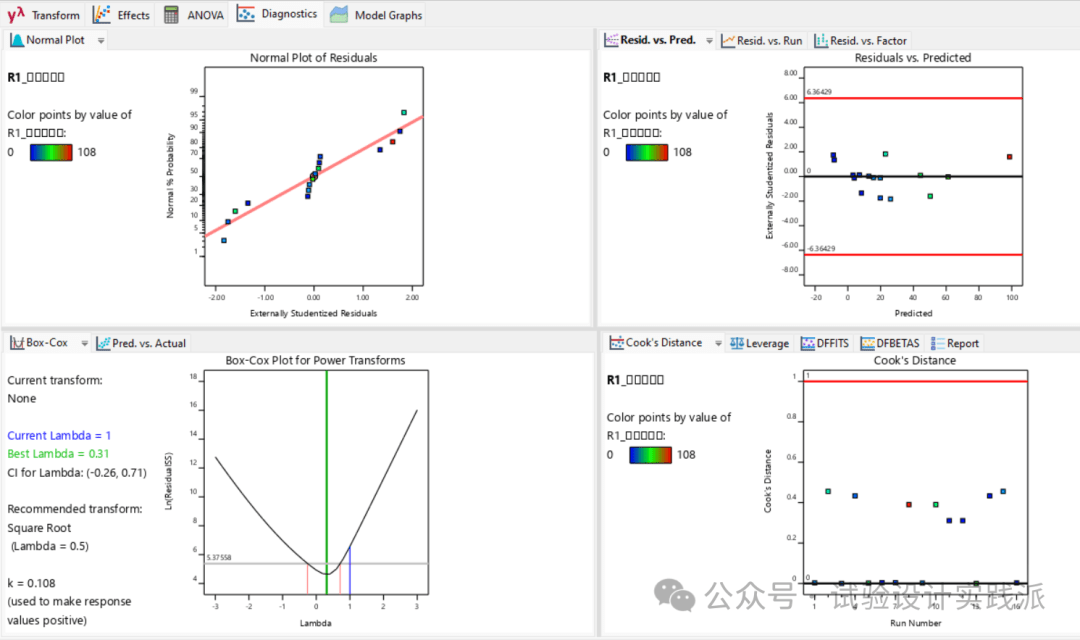
  • 正态概率图（左上图）：数据点呈现“抱团”现象，不够随机，未达到理想的直线分布（虽然非典型的S形）。值得注意的是，在原始32次试验的分析中此问题未出现，可能是本案例直接使用了两次重复的平均值所致；
  • 残差与预测值（右上图）： 分布相对均匀，未观察到明显的漏斗形或喇叭形；
  • Box-Cox转换（左下图）：Design Expert基于Box-Çox分析，建议进行平方根（Square Root）转换。
图片
一般来说，残差检验出现以下情况时，通常需要考虑进行响应变换(Response Transformation)：
  • 残差正态概率图，出现S形等情况
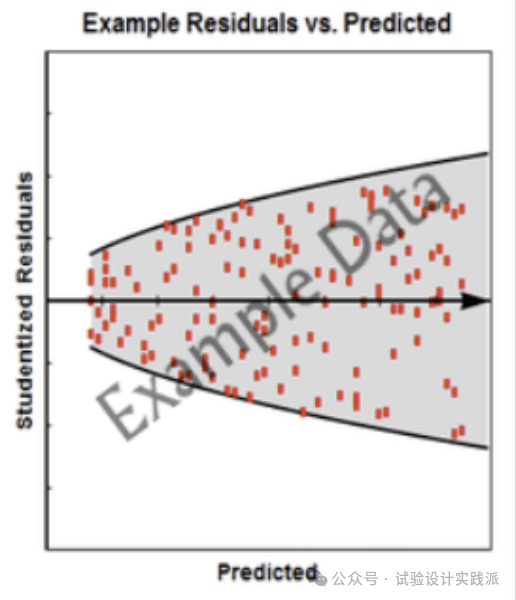
  • 残差与预测值关系图，出现漏斗形或喇叭形等情况，如下图所示。
    图片
本案例残差图的异常迹象（如正态图“抱团”）相对而言不够典型和直观（例如不如残差vs预测值呈现清晰的漏斗形那么一目了然）。未来将单独分享一个响应变换效果更显著的典型案例。本文聚焦于：如何使用Design Expert便捷地执行响应变换，并对比变换前后分析结果的差异。
 Design Expert响应变换操作
我们直接遵循Design Expert的建议，对响应值进行平方根转换，然后重新进行ANOVA分析和残差分析。
在试验设计DoE软件：Minitab和Design Expert中，我们曾介绍过Design Expert的一些独有或更具优势的功能，其中“操作简便的响应变换”便是一项。需要变换时，只需要打开软件“transform（变换）”标签页，选择残差检验中给出的变换方式即可。
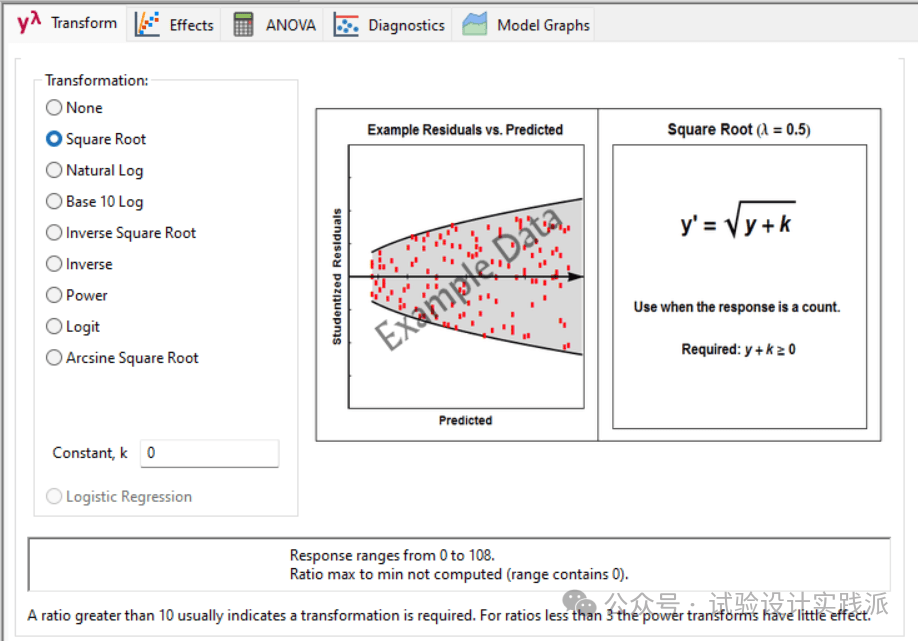
Design Expert还提供了一个实用的经验法则（如下图所示）：通过计算响应变量的最大值与最小值之比(Ratio = max / min)来初步判断变换必要性。Design Expert会自动计算该比值。经验表明：若比值大于10，通常需要进行变换；若比值小于3，则幂变换(Power Transformation)的效果往往微乎其微。(下图原文：A ratio greater than 10 usually indicates a transformation is required. For ratio less than 3, the power transforms have little effect.)
图片
注：本例中因存在响应值为0，比值计算不适用，需依赖残差图和Box-Cox分析）
变换效果对比
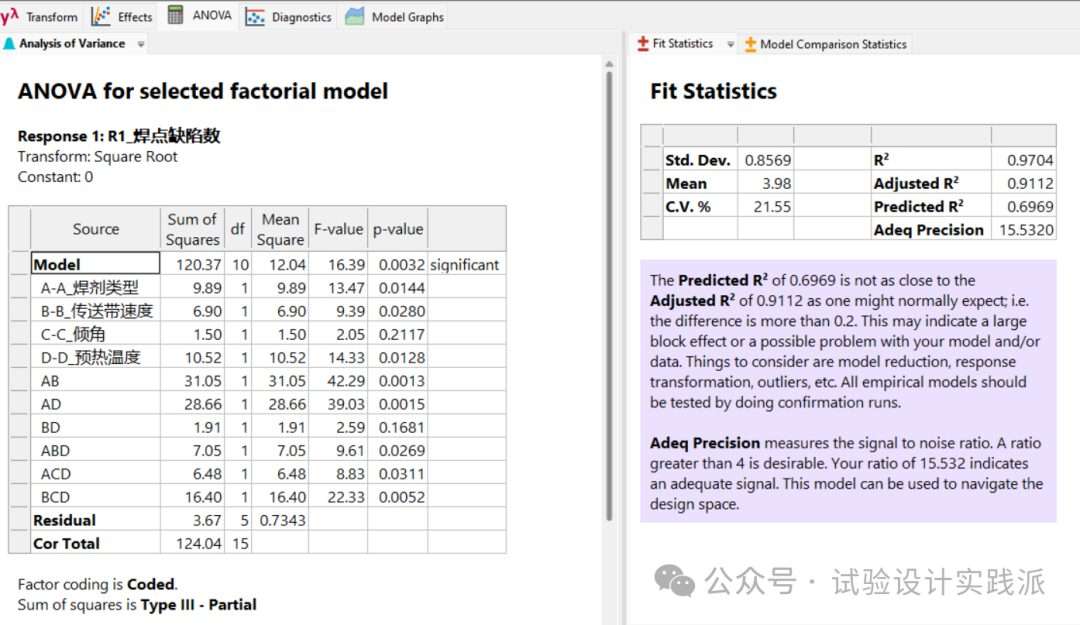
完成平方根变换后，我们在Design Expert中重新执行了ANOVA分析，并基于效应显著性及工程重要性进行模型简化。
本案例中，模型简化并没有新鲜结论，最显著的依然是交互作用AB，AD和BCD；然而模型拟合得到了明显提升，预测R²（predicted R²）从变换前的0.42大幅提高到了0.70！
图片
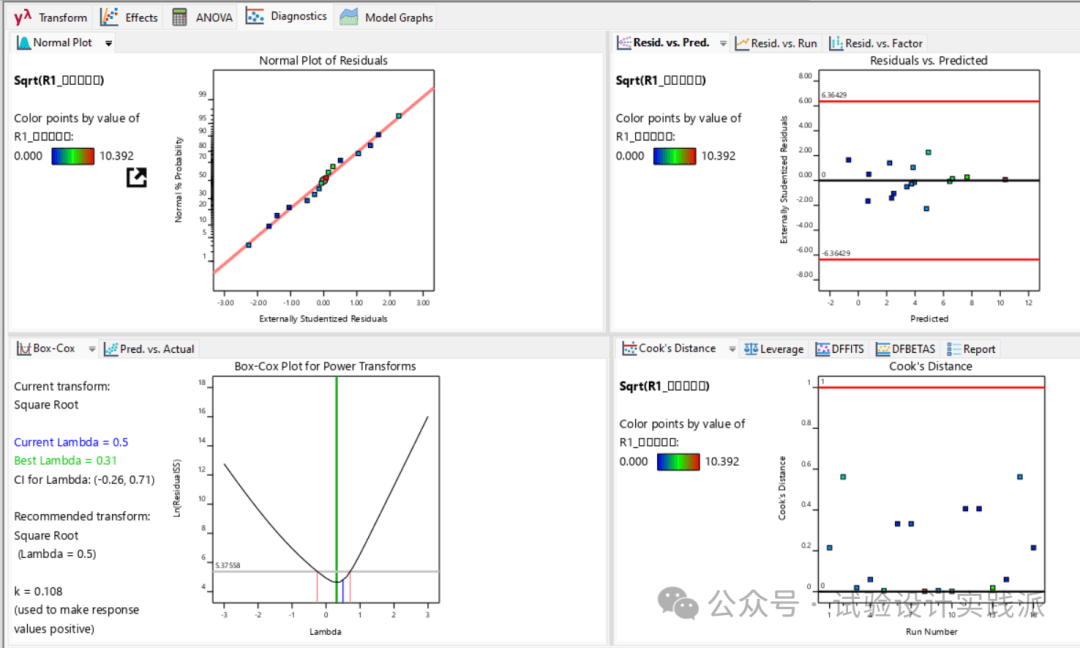
变换后的残差诊断图如下图所示。最直观的改善体现在正态概率图上，数据点更接近直线，表明残差的正态性假设得到更好满足。
图片
文章总结
1. 变换便捷：Design Expert内置Box-Cox变换功能，实验者能轻松执行变换并直观评估变换效果。
2. 变换依据：本案例中，响应最变量存在最小值0（导致max/min比值失效），由于残差正态概率图分布不佳，Design Expert的Box-Cox分析推荐平方根变换（Square Root）；
3. 变换之后重新进行ANOVA分析和模型简化，最显著（均方前三名）和最重要（效应值前三名）的依然是AB，AD和BCD； 
4. 变换之后，模型的预测R²（predicted R²）有明显改善，即模型预测能力——用实验模型预测新试验中的响应——有明显提升；这是该案例中，响应变换的价值所在！
5. 变换之后，残差的正态分布有明显改善；
下集预告
在本案例中，响应变换显著提升了Predicted R²并改善了残差正态性，效果明确，只能算“have some effect”。然而，其提升幅度（如Pred R²从0.42到0.70）虽显著，但尚未达到某些案例中那种“颠覆性”或“化腐朽为神奇”的程度，即没有达到“have significant effect”。
颠覆性的变换效果，往往与“可消除的交互作用”密切相关。因为交互作用(Interaction) 是理解流程/产品复杂性的核心钥匙，也是DoE方法的核心优势所在。响应变换有时能通过改变尺度，使重要的交互作用更清晰地浮现或被更简洁的模型描述。关于响应变换如何更深刻地影响交互作用的解释与模型简化，未来将单独分享一个典型案例。敬请期待！

如果本文对您理解和应用响应变换有所帮助，欢迎点赞👍、推荐❤️！也欢迎分享📣给正在学习DoE的同事朋友。

文中若有任何疏漏或您有宝贵建议，请务必在评论区留言指正，您的反馈是我持续进步的动力！