分析阶段part 1, 包括3.1 和 3.2, 其中3.1是量化CCR和关键设计因子的关系(核心是CTQ流下树&能力流上树),3.2是量化问题及确定重要因子(核心工具就是比较,分析的本质是比较,假设检验是一种高级的比较工具)
分析阶段par 2,包括3.3 量化设计关系(使用的工具是相关性分析和回归分析),3.4设计FMEA,3.5 系统设计优化分析(工具是TRIZ和普氏矩阵)。
关键知识点:
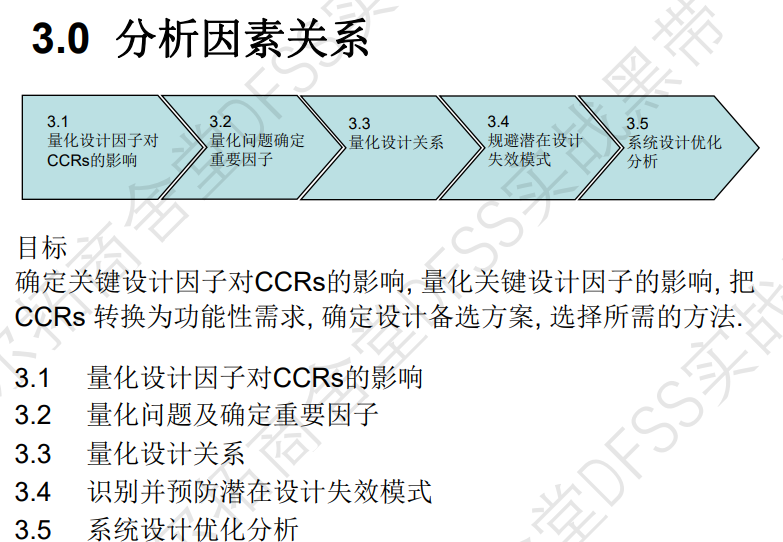
- 关键参数管理CPM:建立“需求”和“能力”之间的相关性。
- 分析阶段是分析因素关系,即“确定关键性能参数与关键顾客需求CCR的关系”,先从CCR到CTQ,再从CTQ到关键性能参数,
- 可选的工具和技巧:相关性分析和回归分析,critical concept, flow-dow, DFMEA
- 关键输出:量化变异性(问题的清晰表述),因子x的优先级排序(有点像之前的SOV分析),传递函数(Y和x的关系),CTQ流动图,FEMA文档
- 现代设计关键在于量化数学问题(前面有一个前提,就是提出假设,也就是量化的目的是什么)
- 系统功能设计:功能分析(如何把设计问题量化为数学问题),TRIZ创新发明,Pugh矩阵优选迭代。
- 如何进行有效的对比,既要看平均值,又要看波动。这就是六西格玛思维。
- 统计基础知识:均值,标准差,正态分布,中心极限定理
- 中心极限定理:从任意随机分布(不要求正态)中随机抽取N个样本,计算其平均值xbar,xbar的分布,随机抽样量N达到5个(如果是均匀分布)最差30个(指数分布这种严重偏斜分布),xbar的分布都会变成正态分布,其标准差差=总体标准差/sqrt(N),或方差=总体方差/N。这是很多实际抽样的理论基础(当然前提是你要用抽样均值进行基于正态分布的假设检验)——2023-7-13
- 3.0和3.1偏理论和抽象,值得多看几遍,3.2是基础统计检验,需要用minitab练习;
- 3.2 涉及到了比较法、假设检验、置信区间、独立性检验、正态性检验、一对一均值比较,方差对比(一对标准,两个之间),多重比较等。
备注和笔记:
- “关键参数管理CPM”:建立需求和能力之间的相关性,这就是胶带产品开发中,“应用性能”和“材料性能”之间的相关性;又分成几个层级:产品整体、胶层、胶水配方。应用性能包括客户端使用产品的性能,可制造性(工艺部门的生产需求)。
- 课程所讲案例,更多是针对工程技术问题,可以做功能分析,可以用TRIZ; 有物理层面的层级关系,比如系统——子系统——组件等,就像手机设计。
- 第一步确定关键性能参数CTQ与关键客户需求CCR的关系,即产品的性能如何与客户的应用需求联系起来。联系到最近在解决OCA项目中的rework issue,CCR就是rework property,我现在的关键就是找到材料本身性能和rework的关系,明确之后才知道如何改进材料配方,不然就只能把能做的一直试错,但试错是没有止境的,可调的因子太多。 2023-2-26
- 如果第一步不清晰,就需要用3.2的比较法和假设检验,构建假设,验证假设,从而明确CCR和哪个或哪些CTQ相关。(假设思维!分析的本质是比较!)
- 第三步,找到CTQ和更低层级的关键因子之间的关系,常用的工具就是相关分析和回归分析,因为一般会涉及到多个关键因子。(假设思维,高级分析是相关性和回归分析)
- 找到关键设计因子—》CTQ—》CCR之间的逻辑关系之后,之后就是设计FMEA,研究潜在的失效模式、潜在后果和预防措施等;
- lean six sigma is not work harder.
- lean six sigma is not work faster.
- lean six sigma is to work smarter.
- 功能分析,对应于具有子系统、组件的产品,比如自行车、汽车、手机等;但对于我做化学产品开发,是一个配方和工艺参数调整,不会存在组件和功能之间的功能分解图,更多是一种DOE分析,建立x(配方含量,工艺参数)和y(产品性能)之间的量化关系,特别是交互作用等。 2023-2-26思考
- 假设检验,要重读《六西格玛统计指南》蓝皮书
3.0分析阶段概述 (第18讲)
分析阶段的目标:分析x(关键设计因子)和y(CCRs)的关系,量化关系,把CCRs转换为功能性需求,再对功能性需求进行进一步分解,寻找和更基础的子系统或组件的特性之间的相关性;确定设计备选方案,选择所需的方法。
关键词:量化、相关性、DFEMA
传统设计vs现代设计:现代设计关键在于量化数学问题。
系统设计(田口第一段设计)在A阶段的三个主要任务
- 步骤一:功能设计(分析关键因子、量化设计关系、风险分析——将设计问题转化为数学问题)
- 步骤二:创造性设计 (TRIZ创新发明理论)
- 步骤三:系统设计迭代优选(普氏矩阵优选 Pugh Matrix)

第18讲 3.1量化设计因子对CCR的影响 (2023-2-26)
3.1 量化设计因子对CCRs的影响
本讲内容:功能分析,功能框图,CTQ需求流下树,传递模型,建立CCR和关键设计因子之间的关系。
说明:并非所有的需求都要进行流下树分析,而是面向关键需求,特别是来自于QFD得到的关键需求。
客户需要的功能——> CCR 关键顾客需求 ——> CTQ 关键性能需求 ——> 设计因子,量化相关性
功能架构分析:
- 功能定义:“主谓宾”(主体+动作+客体)的功能描述,TRIZ中function analysis也以此为前提。
- 功能分解:功能分类分组、逻辑关系、功能链条,主要功能和从属功能 (绘制方法:功能树、功能系统图)
- 功能框图(功能模块化,区分基本功能与从属功能,功能重要性排列)(功能之间也分上下级关系或并列关系)
- 量化评估:建立Y=f(x1,x2,x3,…)的转换函数
功能分类:(和FMEA相似,先梳理产品的组成、功能,再做FMEA)

功能框图(功能系统图):对产品进行功能分析(比结构分析更抽象)
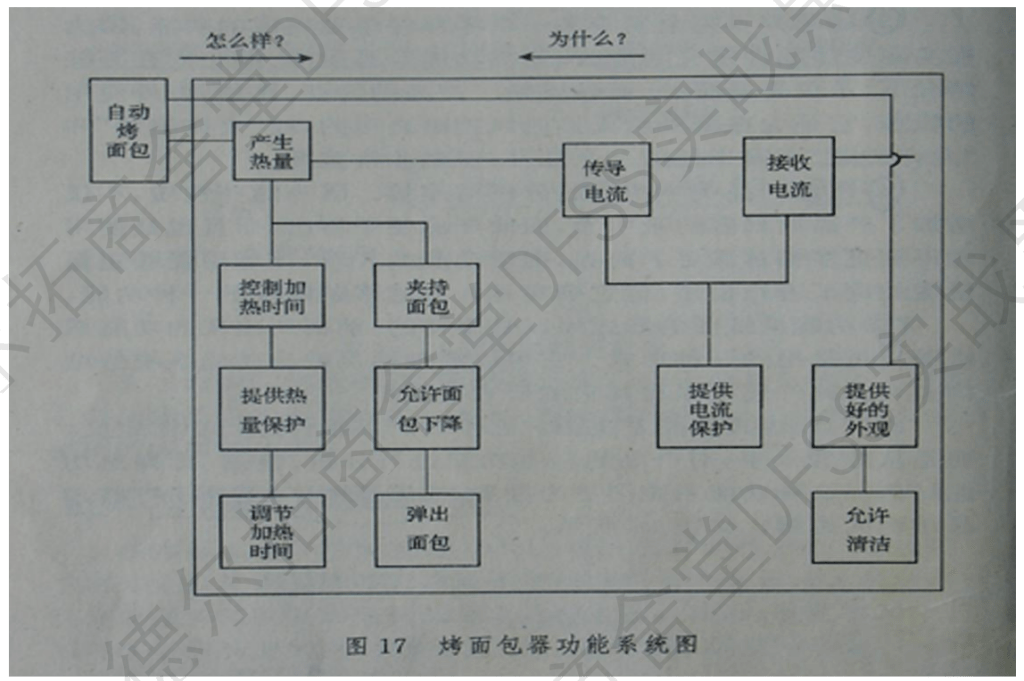
转换函数: 大Y —> 小y —-Xs之间的层层转换
CTQ向下流向图:客户需求,如何一步步传导到系统需求、子系统、组件的需求。
针对关键的客户需求(比如质量屋中的output,DFMEA中RPN最高的,等),进行CTQ层级分解。
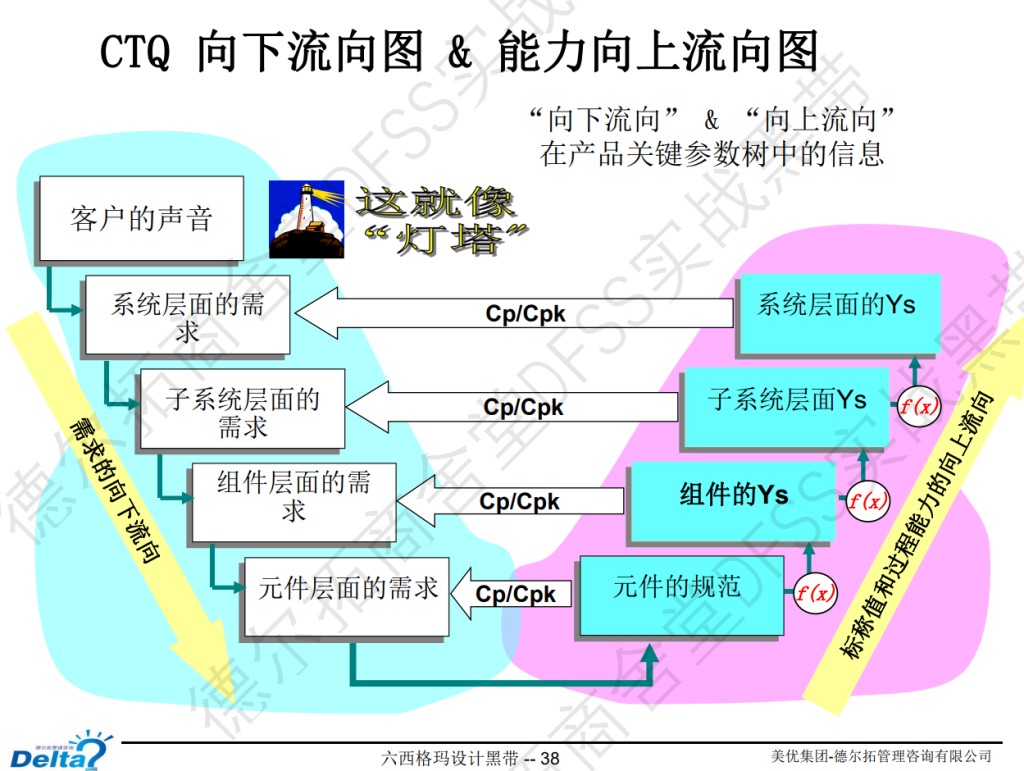
转换函数,从一开始的输入,到最终优化设计后的聚焦关键参数。
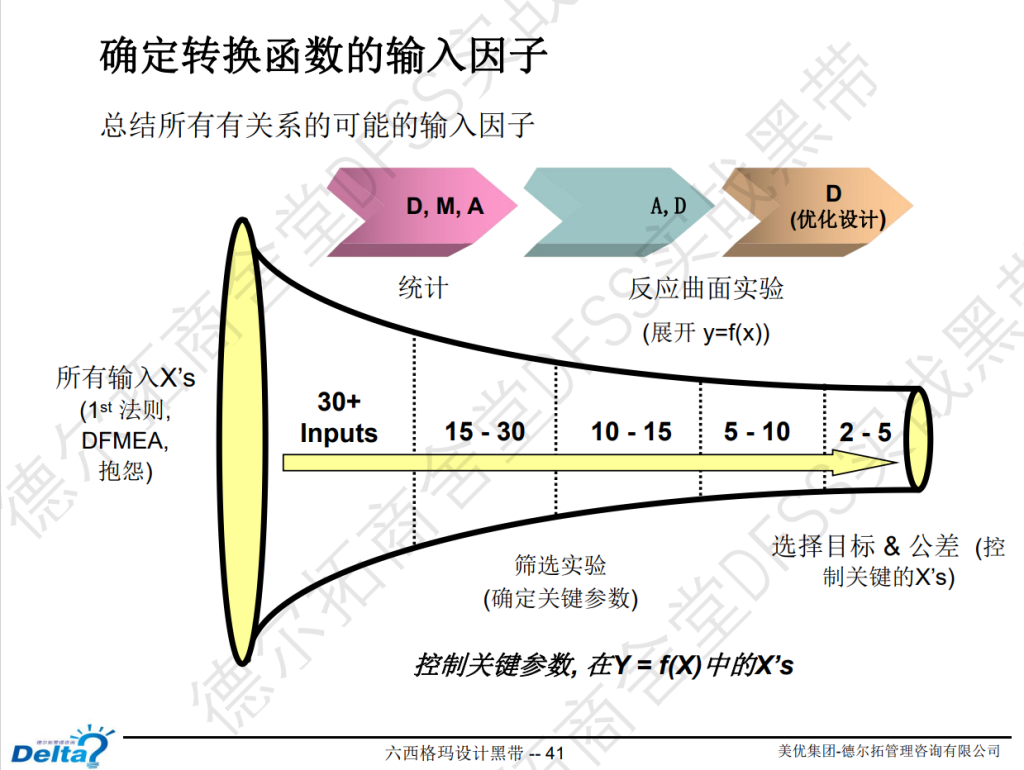
如何发现数据之间的联系,常用的方法:两两比较、相关性和回归分析、等。
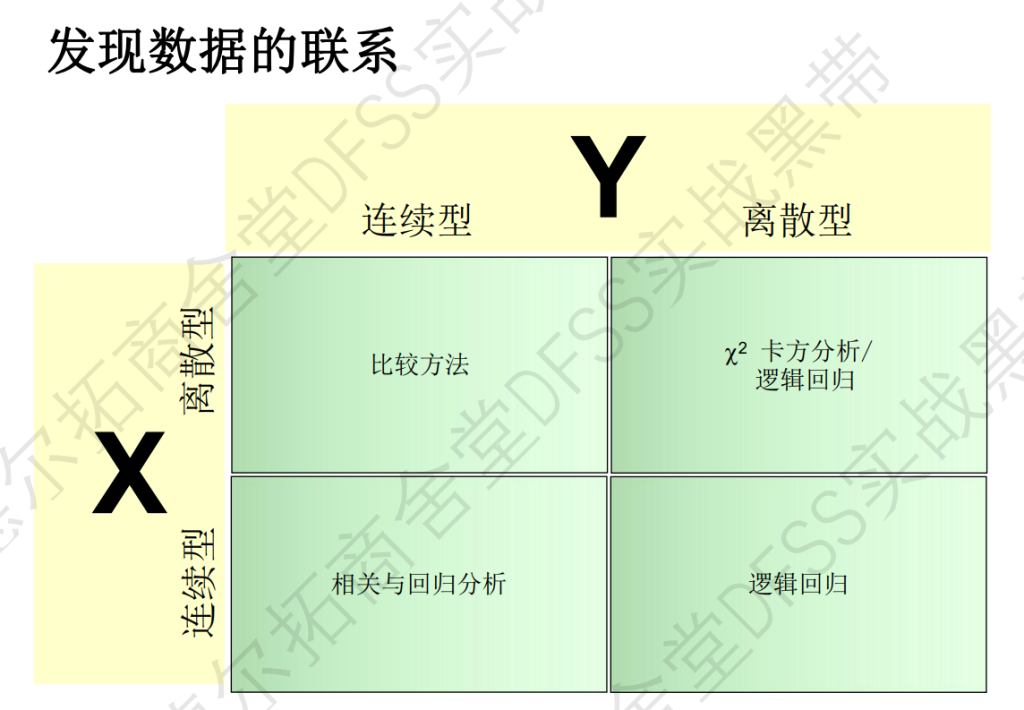
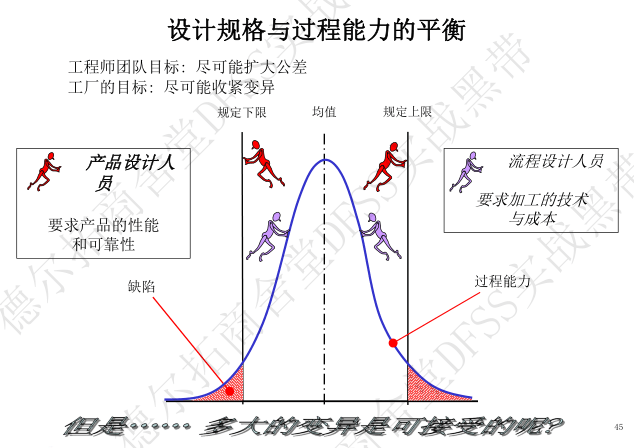
2023-7-12 重读第18讲
第19讲 3.2 量化问题及确定重要因子 (2023-2-26)
关键词:假设检验,对比法; 简单对比法依然是一种量化工具!
目标:使用对比法找到关键设计因子和CCRs之间的关系,从而建立转换函数。
关键议题: 比较方法,假设检验,置信区间,独立性和正态性检验,一对一比较,方差比较,多重比较。
使用对比法确定x和y之间有没有关系,而下一讲的相关性和回归分析,确定x和y的相关性有多大。
如何进行有效的对比,既要看平均值,又要看波动。这就是六西格玛思维。
绝大部分的对比都是基于抽样样品,利用样本信息,推测整体的情况,这就是“统计推断”statistical interference。

统计术语:抽样,代表性样本,置信区间(confidence interval),总体参数(u,sigma),样本参数(x,s)
置信区间
置信区间:根据样本计算出一个区间,是有95%的可能性,总体参数的平均值,会落在这个范围内。如下有一个案例,收集198个成年人的耳朵和嘴的距离,计算出置信区间。结果是“根据95%的置信区间,一个成年人的耳朵到嘴巴的距离的平均距离(总体平均值)会落在6.66-6.94英寸之间,这个距离的差距(总体标准差)会落在0.92-1.12英寸的区间内。

抽样样本数增加,置信区间会缩小,如下所示,抽样100次,每次抽样10次和抽样100次的差异。
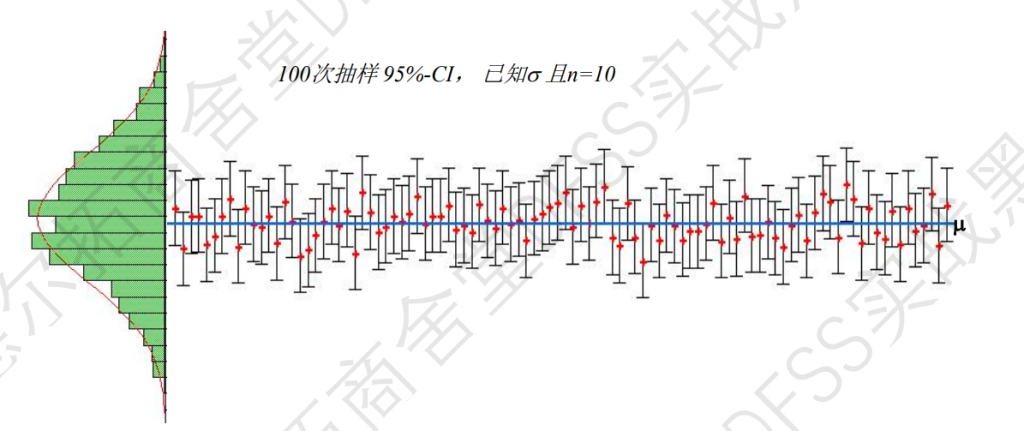
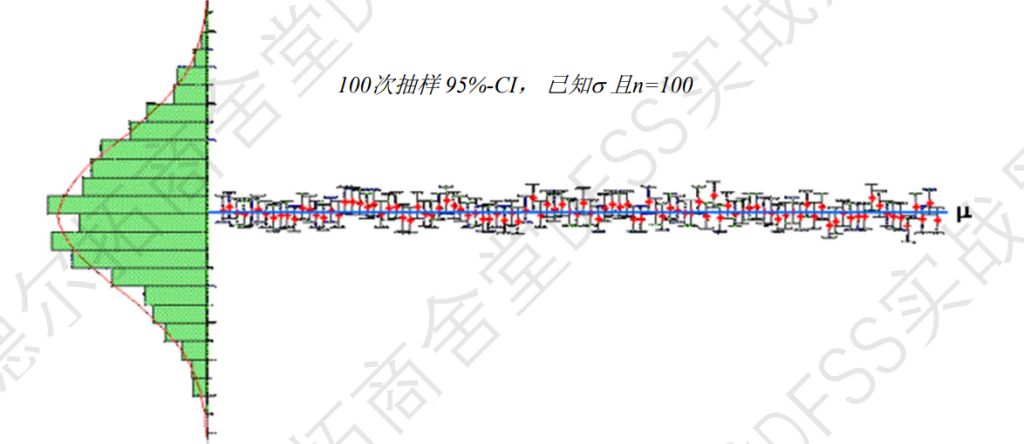
比较方法:
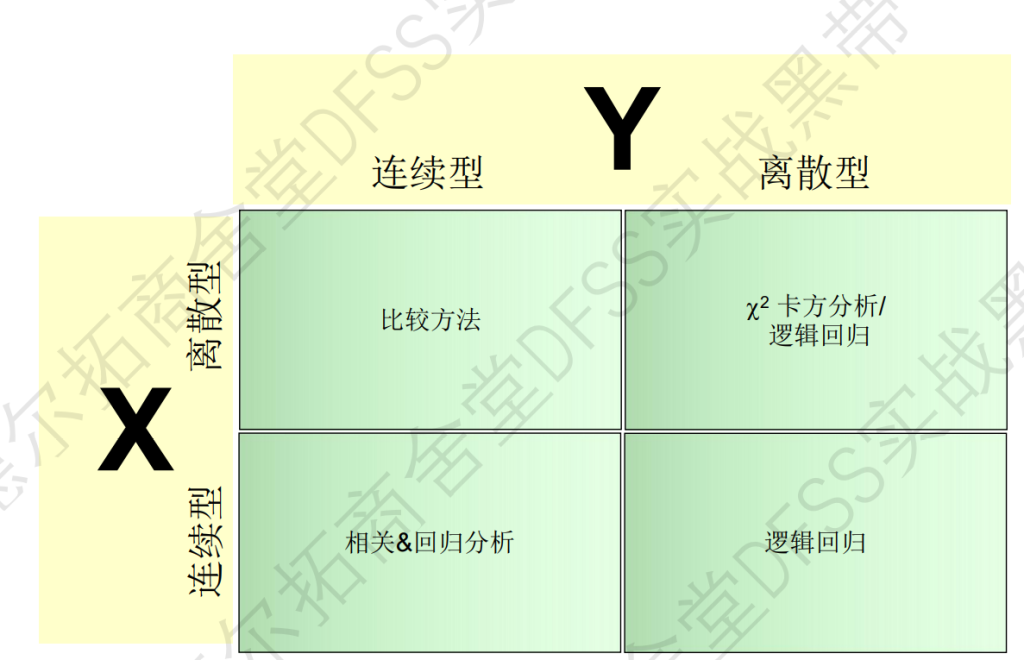
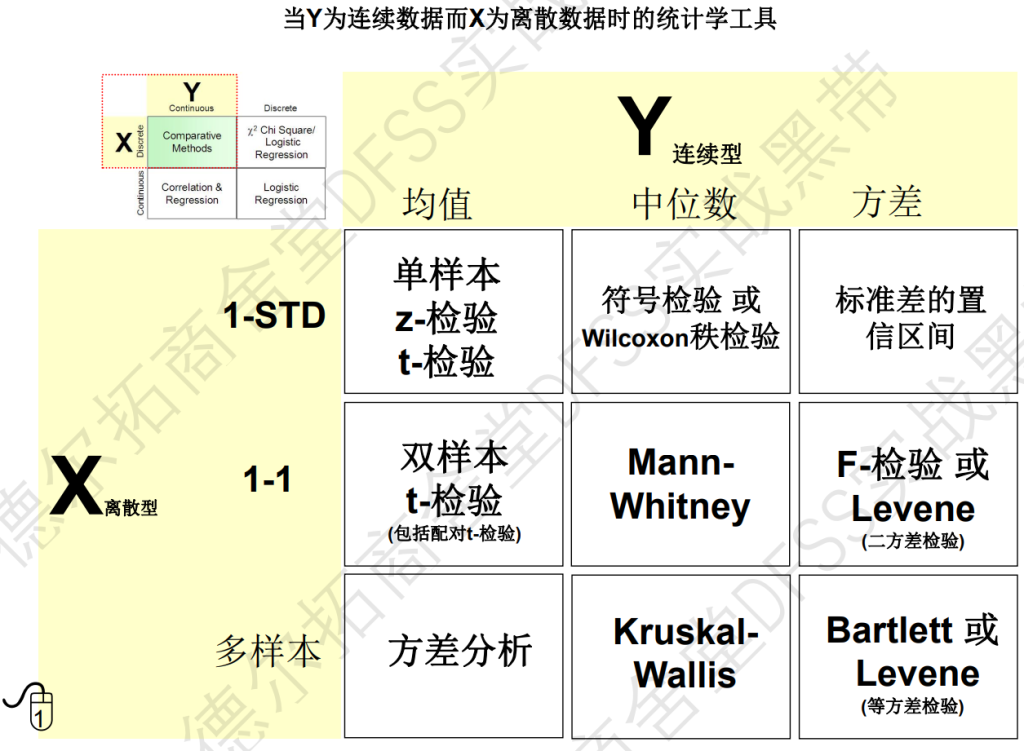
比较的流程:问题陈述——比较参数——建立假设检验——独立性——正态性——构建统计量(均值还是标准差还是什么)——接受还是拒绝——给出最终的结论。
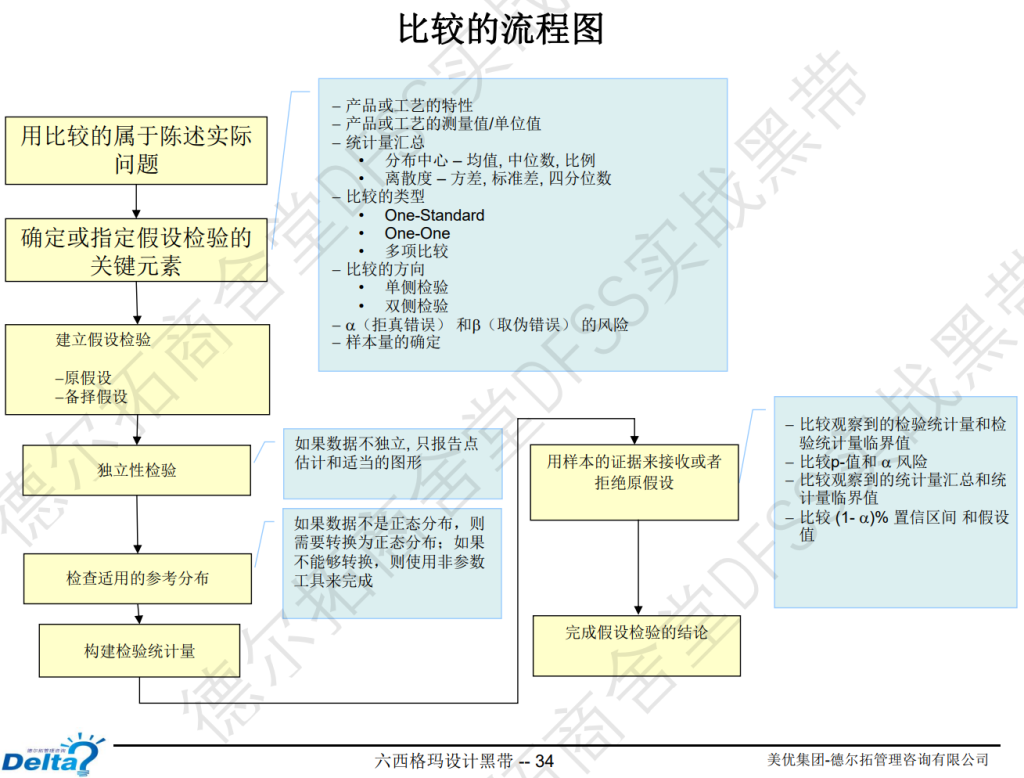
比较类型:
| 比较类型 | 比较方式 |
| 单样本 | one to standard(固定值) |
| 双样本 | 一对一 (比如一个产品中更换一种原料) |
| 多样本 | 多重比较 |
对比陈述:产品的某个特征,工艺中的某个特征,比如尺寸、质量,某一种具体的测量量,可以反映产品的”慢、长、偏、多、胖“的情况。
单侧比较,双侧比较:
拿到一个具体的问题,先抽象成统计学的陈述,明确对比类型、对比统计量、对比方向。
录像:
2023-7-12 重读本讲
3.2 量化问题及确定重要因子
第20讲 单样本均值比较(袁金玲助讲)
为什么要用假设检验:假设思维!所有的试验都是先有假设。
主要内容:假设检验,中心极限定理,单样本Z检验对比均值(平均值vs标准值)(已知总体标准差的情况,这样就可以用中心极限定理计算出抽样样本均值的标准差)
本讲比较简单,主要介绍单样本均值比较,已知总体标准差和总体均值,比较样本均值和总体均值的差异,涉及到单侧检验,双侧检验,检验的两种方法(看p值,看置信区间);
难点:(1)alpha和beta的含义,即两类统计错误,(2)中心极限定理,样本标准差和总体标准差的关系。
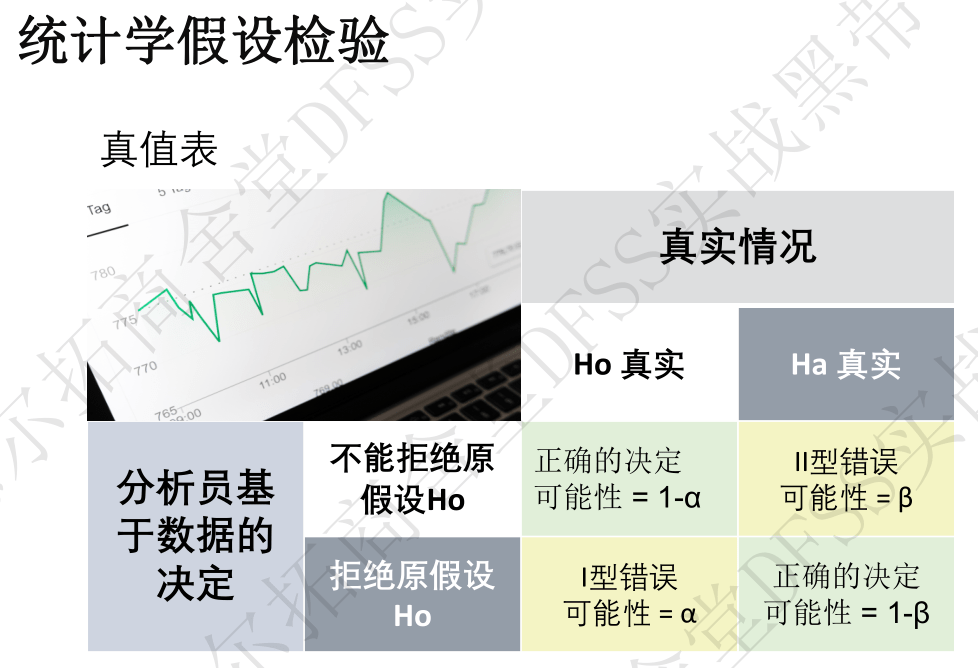



上图:样本的”离散的量度”,即标准差=总体标准差/sqrt(n),当然前提是已知总体的标准差,这样计算的原因就是下面的中心极限定理。
中心极限定理:样本均值,样本标准差,估算总体标准差。
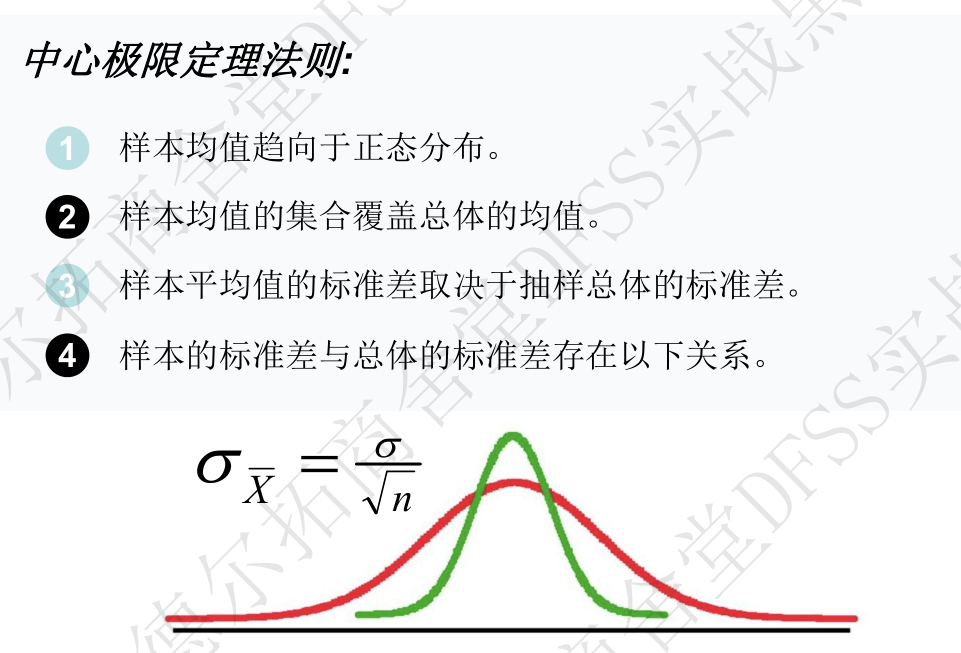
备注:样本标准差为什么要比总体标准差更小?注意样本均值和样本标准差,都是。比如N=1时,样本标准差=总体标准差,此时的含义是,每次取一个样本,重复取样,计算均值和标准差;如果N=5,代表的不是取5个样本计算样本均值和标准差,而是重复取5个样本,得到每次抽样的均值,然后计算均值的均值和标准差,这样5个样本的均值统计上就会小于一个样本的均值,自然重复取样下的标准差也会小于总体标准差。_2023-7-13
之前的总结:统计基础知识:中心极限定理, (x bar = 从总体X中随机取出n个x,其平均值),复制一个图片在这儿理解。
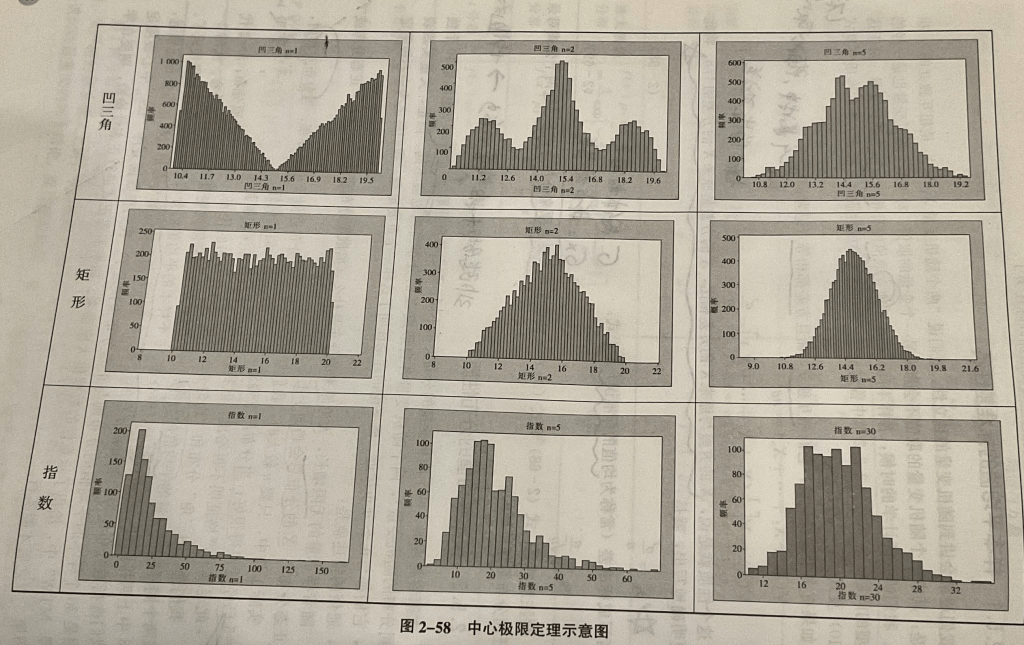
标准正态分布(Z分布)
one-to-standard:单样本比较
假设检验:如果(1)p值是否小于0.05,(2)置信区间是否不包含要检验的数据,推翻原假设(零假设)

2023-7-13 出差错过直播,没有看回放;直接重新过一遍pdf讲稿;统计比较-单样本均值比较,基础知识。
第21讲 2023-3-5 张玮助讲
本讲内容:假设检验,独立性检验(时间序列图,游程检验),正态性检验(总体标准差位置的情况,不用Z检验而要用t检验的情况),一对一的均值比较。
上一讲是最简单的已知总体标准差的情况,本讲是更普遍的未知总体标准差,和t检验情况。
t检验
One-to-standard (单样本) 均值检验,总体标准差未知,根据分布,分别选择:
- Z-检验 (正态分布)
- t-检验 (t分布,样本量较少,不适合用正态分布,t分布与样本量n相关,见以下的t分布公式)(直接根据样本的数据计算出样本标准差s(注意根据单次抽样的样本标准差算不出总体标准差的,除非连续重复抽样,然后用中心极限定律反推)
- minitab:进行Z检验时,需要输入总体均值;进行t检验时,软件直接计算出s使用。

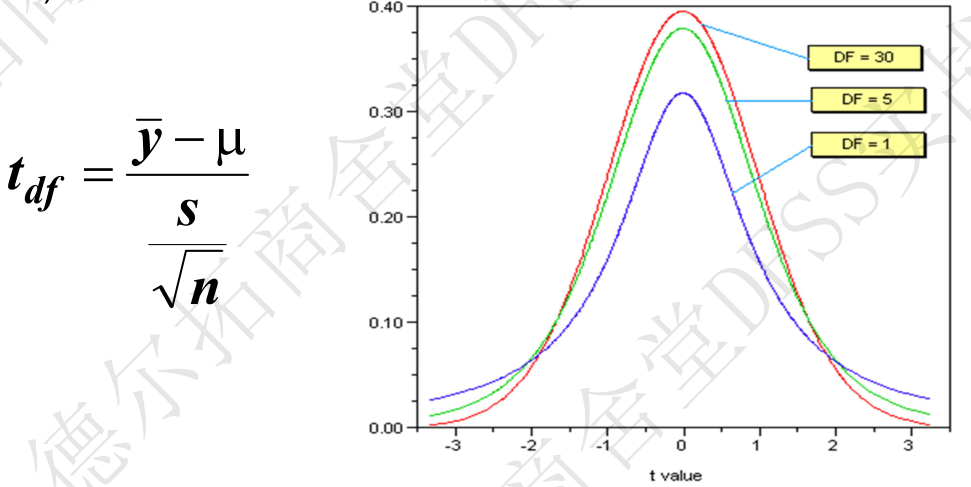
minitab操作:数据,确定标准值(均值),选择备择假设,输出p值=0.009<0.05,拒绝原假设。
独立性检验
如何判断数据是否独立:可以查看SPC中的数据趋势(minitab操作中的”图形>时间序列图“,判断是否有数据扎堆的现象),使用“游程检验”判断数据是否独立(零假设:数据是独立的,即数据不存在某种顺序),
游程检验:先使用“图形化汇总”计算中位数,然后使用“统计-非参数-游程检验”,输入中位数,p<0.05,拒绝原假设,数据是非独立的;如果p>0.05,就不能拒绝原假设。
原假设:数据是独立的。 p<0.05,推翻零假设;否则不能推翻。
原理:游程检验,为什么不用均值,而要中位数? 因为中位数将数据数量一分为二,计算两侧的游程,进行”非参数检验“。
如果数据不独立,说明数据是以时间为序的,此时应该尝试解释这种数据和时间的关系;不独立的数据,不适合中心极限定律(样本均值的方差等于总体的方差处于样本量)和假设检验。
正态性假设
无论标准差是已知的(使用标准正态分布Z查表)或者标准差未知(使用学生t分布查表),我们都依赖于中心极限原理的特性:随着样本量的增加,样本均值趋向于正态分布。
原假设:数据是正态分布的,(原假设是期望的结果)
操作:统计——基本统计量——正态性检验 (默认使用A-D检验即可)
拒绝是有说服力的,没法拒绝是没有说服力的; 为什么游程检验和正态性检验,常见的结果都是p>0.05,无法拒绝零假设,所以数据是独立的,或数据是正态的?
提醒:Box Cox 变换 – 对于非正态的数据转换成正态数据
练习: 弹弓数据, 时间序列表,正态性检验(发现p<0.05,数据不正态),使用Box-cox转换。
!!!功效与样本量问题 (需要反刍)
统计功效:拒真概率=1-beta,
容忍度delta: 什么含义,容忍度很大,两个分布分开更多。容差很大时,beta风险很小;容差很小时,beta风险变大,就需要增加样本量来降低风险。
不能拒绝是没有说服力的,此时的风险,可以通过增加样本量来缩小,增加样本量时分布会变瘦。
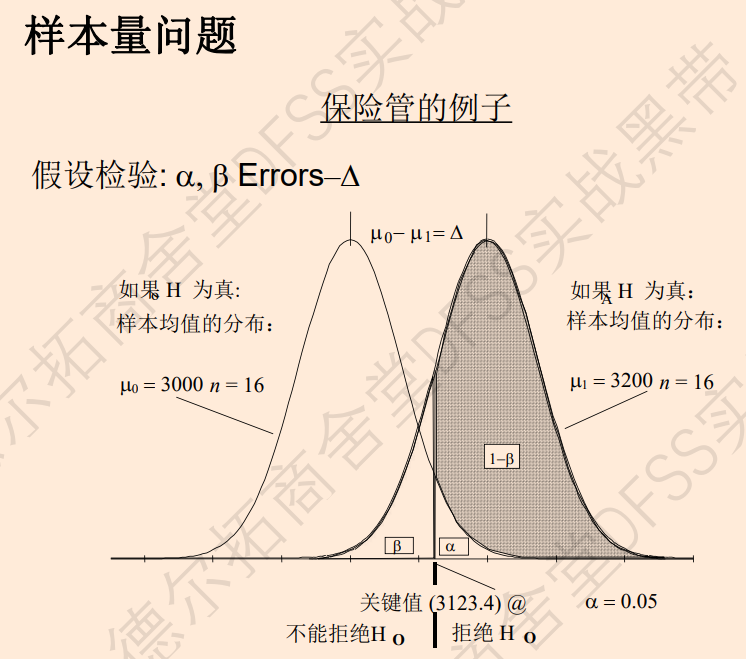
样本量设定多少,才能?降低beta风险。(已知标准差、功效值,差值,计算需要的样本量)
容差设定:0.5-1.5倍sigma,通常选择1倍标准差,容差是我们能接受的误差。

练习:cycleties.mtw,样本均值和9.5对比,备择假设是均值<9.5, 单样本t检验,p=0.277,无法拒绝零假设;此时需要确定“检验功效”,是否支持我们接受零假设;如果功效不足,需要将样本量增加多少?
minitab“统计——功效和样本量数据——单样本t”,功效只有0.144
功效检验的零假设:
如何批量计算出不同的容差(delta)达到不同的功效下需要的样本量。
one to standard方差(标准差)比较
使用方差评估数据的波动程度和变异量;然后使用卡方分布比较方差。
卡方分布和数据量有关,是一个偏斜分布;数据量越小,分布越倾斜; 数据量增加,逐渐接近正态分布。
使用95%标准差的置信区间(图形化汇总输出),判断是否拒绝原假设(标准值standard是否落在置信范围)。

2023-7-13 过完第21讲,功效和样本量还需要重复。
第22讲 3.2 量化问题及确定重要因子 2023-3-5
助讲:张望梅
内容:方差比较,多重比较,假设检验的实战和常见问题
单样本的方差比较,用卡方分布:双样本的方差比较,用F分布(两组数据都是正态的)。
主要内容:F检验,方差检验,实践
双样本方差对比
原假设:两个样本的方差相等。
“统计-基本统计量-双样本方差”,查看F检验的p值,p=0.707,不能拒绝原假设。
先做正态性检验,输出F检验的p值;如果没有选定正态分布,会输出Bonett & Levene检验的p值。
一对一均值比较,即双样本均值比较。
成对比较:特殊的双样本均值比较,可以转化成单样本均值比较。
举例:电池铝塑膜,热压前后的厚度变化,要求厚度变化控制在3um以内;应该如何进行实验? 这是一个很好的成对比较的例子,一是同一位置的厚度变化,从而充分很多误差的干扰; 二是关注200片如果已经是总体样本,就不需要做假设经验了。
多重比较 方差对比
p<0.05, 拒绝零假设(多组样品之间,没有方差差异),说明至少有两组的方差是不相等的。
多重比较:均值 ANOVA (单因子方差分析)
实际场景,比如多个供应商,多个设备,多个工艺之间的比较。
ANOVA的关键是控制总体风险,而不是只控制两两比较之间的风险。
非参数检验: 功效比其他检验更弱,这儿主要讲的是中位数的比较,细节略,以后需要再研究。

案例:电池膨胀的竞品分析,竞品样本量很少,此时就要用非参数检验,评估热压之后的”膨胀值“,对比产品之间的差异。
假设检验的几点强调:
- 统计显著和工程显著之间的差异,需要详细分析;统计学工具,还要结合具体的工程经验、技术规范,才能给出具体的结论。而不是单纯看统计数据。
- 做假设检验的目的是什么,要解决什么问题?关键是要解决实际的工程意义。
- 假设检验:用样本统计量,推测总体统计量。
- 正态检验和游程检验(独立性检验),其实也是一种非参数检验。
- 何时使用假设检验——涉及到比较时,都可以考虑应用假设检验。【分析的本质是比较,比较要用假设性检验!】

2023-3-5 完成3.1和3.2学习,后续整理发布。
2023-7-13 跳过最后第22讲,发布本部分学习笔记。