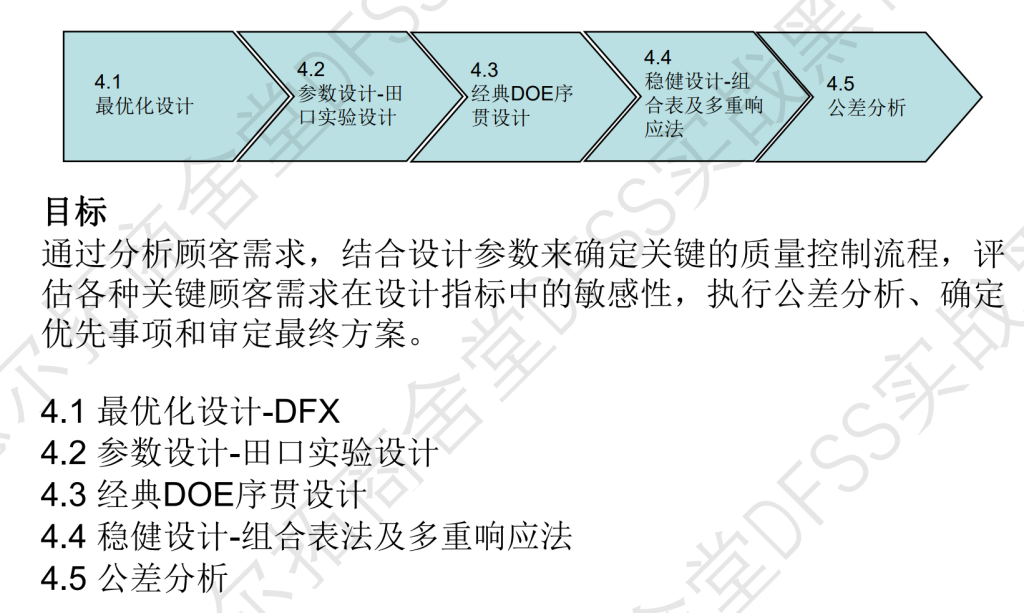
设计阶段概述:
DMADV的stage 4 Design(设计阶段),包括参数设计和公差设计这两段设计(田口三段设计的后两段)。第四步分成三部分
- part1 : 包括4.1 (几乎忽略),4.2 稳健设计- 田口实验设计,4.4 稳健设计-组合表法,多重响应法;这一部分汇总了三种稳健设计(田口、组合表法、多重响应法)
- part2: 4.3 经典DOE序贯设计——重温(和DMAIC内容一致)
- part3 :4.5 公差设计——对我来说全新的知识点
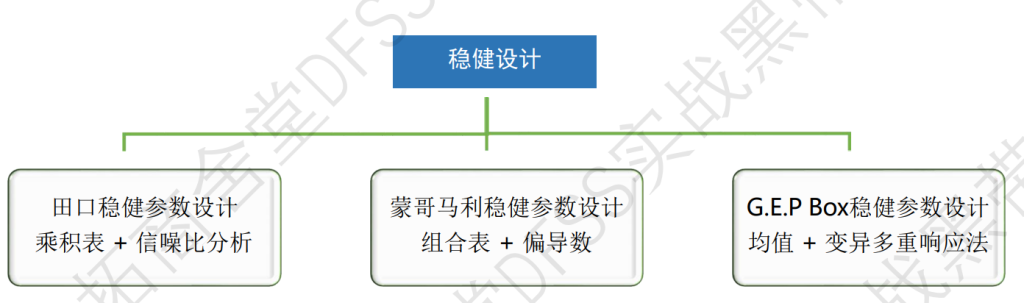
参数/稳健设计,包括三种方法:(1)田口乘积表法,(2)蒙哥马利组合表法,(3)Box多重响应RSM法。
重点是第31讲,稳健设计的基础知识;其次是三个稳健设计的方法对比。
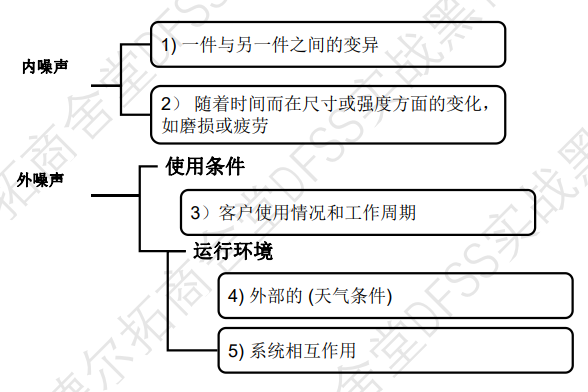
- 关键知识点1:噪声变量的分类,实验中都有哪些类型的噪声变量,这也是稳健设计的前提。
- 关键知识点2: 三种稳健设计的区别和优缺点,田口实验设计更老派(乘积表,试验次数多,只考虑主效应,缺乏统计预测),组合表法(将噪声作为X的经典DOE,可分析交互作用等高阶项,利用交互作用进行脱敏,使用统计模型预测),多重响应法()
- 对应稳健设计,可以在经典DOE设计之后,补充噪声因子下的实验,比如田口设计;也可以一开始就识别出噪声因子,然后直接将噪声因子作为实验因子进行析因设计。
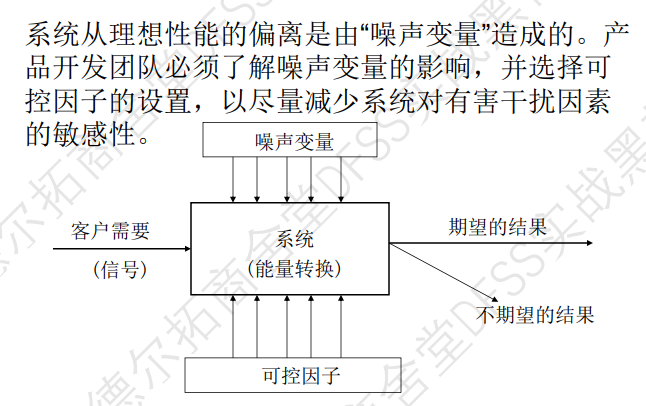
- 在田口实验设计中,会使用”参数图P-图“,通过研究参数图,分析实验的输入、输出、可控因子、噪声因子、等,然后再针对可控因子和噪声因子进行田口实验规划; 注意参数图是很多实验的关键,包括之前参加DFMEA培训,针对”任务功能“,也需要分析参数图,然后根据输入、输出、控制因子、噪声因子等,分析失效模式(不能达到输出)、失效原因(逐一核查控制因子和噪声因子)
DOE中的一些提醒:
- 图形化汇总:进行设计时,使用”图形化汇总“查看响应变量的范围,是否覆盖了我们想要的目标值。如果目标值在范围内,那就是个好消息,避免了爬坡,可以在现有的试验空间内进行优化。
- 中心试验的目的,何时需要手动增加中心点试验,比如从线性模型(发现存在弯曲)到非线性模型,比如量化模型误差。
还没学清楚的内容:Excel规划求解和其中的参数设定,何时需要使用exccel规划求解器。
4.1 最优化设计-DFX (第29,30讲)
这一讲针对硬件类产品设计,设计时考虑制造环节和装配环节,从而改善制造和装配的难度。没有详细研究,后面再看。这是观察硬件产品的新视角。
可制造性设计DFM,装配设计DFA
知识点:
- 功能分析!“零件”数目清单和“接口”数目清单, (五六月份公司的DFMEA培训,培训老师讲接口分析,和这儿的功能分析几乎一样!)
第29讲 – 4.1 最优化设计DFX — 可制造性设计DFM


第30讲 – 4.1 装配设计DFA
实战部分主讲人:施丽琴Luka (4月9号周日第30讲)
DFA装配设计,DFM可制造设计:统称DFMA(制造与装配设计design for manufacturing and assembly)
分析顺序:概念设计–》装配设计——》制造设计——>详细设计

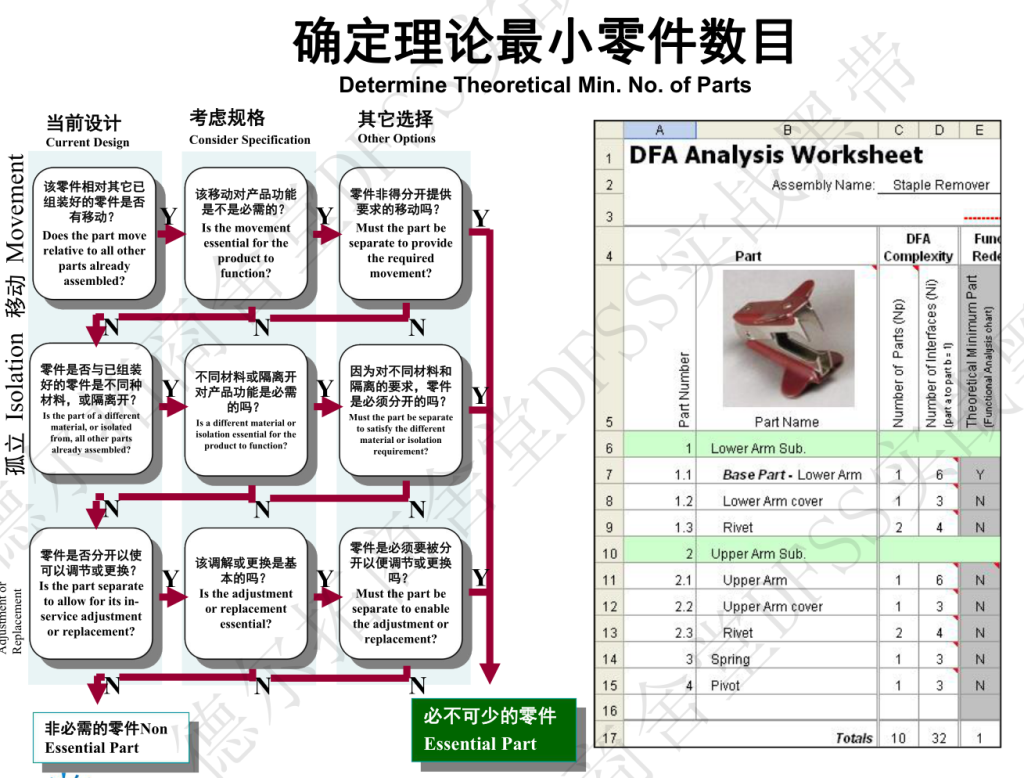
第一步,零部件识别,如何确定某个零件是理论上必不可少的,使用一下checklist! (这也是FMEA中的接口分析的作用,核心就是功能设计;DFA分析之前,要先完成设备拆解图;FEMA也是如此)
案例:订书机起钉器
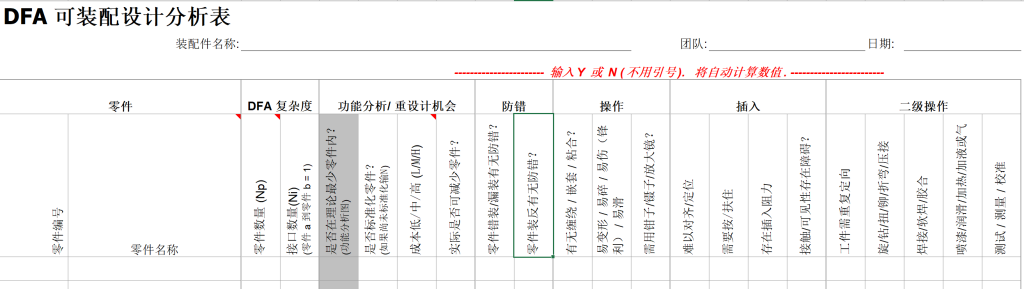
参考附加资料中的“DFA分析表“,如下图:
4.2 参数设计 (稳健设计基础+田口稳健设计)(第31,32,33讲)
2023-4-9直播,31讲是稳健设计基础,32讲和33讲是田口稳健设计;
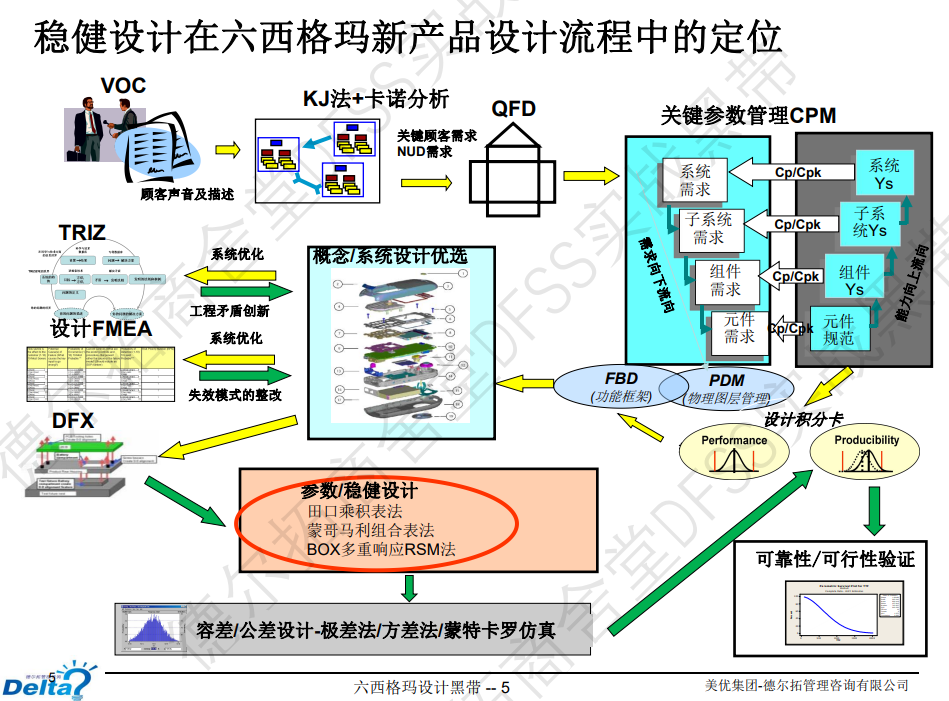
参数设计(稳健设计)是三段设计的中间环节(系统设计,参数设计,公差设计)。
参数设计在DMADV中的位置:
下图中包含三个主线:(1)基于价值的研发,客户导向,(2)田口设计的三段设计思维-系统设计,参数设计和公差设计,(3)DMADV的思维
4.2.0 稳健设计基础 – 原理、概念、应用场景
稳健设计(稳健参数设计):优化参数的设定范围,降低响应的波动程度,也就是降低噪声因子对响应的干扰,使产品更robust。

稳健设计Robus design:研究响应变量和可控因子、噪声变量的关系,确定响应变量的波动最小的参数组合。
稳健设计:既要像经典DOE那样研究可控因子与响应的关系,又要研究”噪声因子“和响应的关系,从而降低噪声对响应的干扰,获得更robust的产品。
实验设计方法的发展过程:反复实验 – 基于经验 – 数理研究 — 统计方法。(现在大家处于什么阶段,应该使用什么工具)
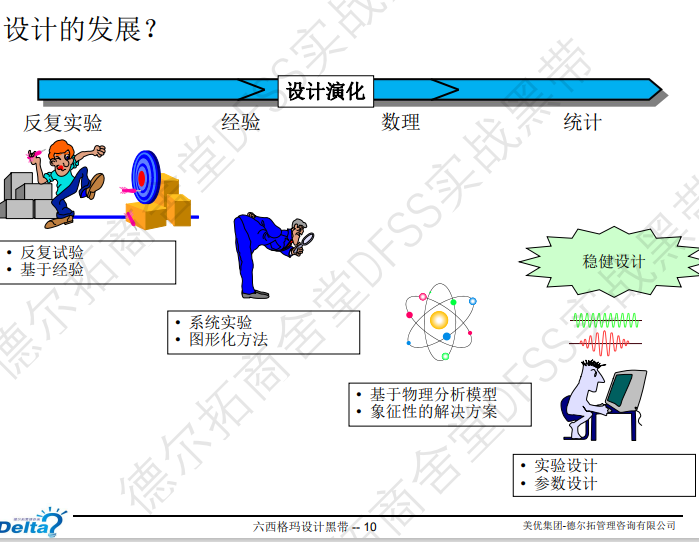
稳健性(robustness),稳健设计,信噪比:

备注:除了田口设计,还有其他稳健设计方法,比如基于响应曲面模型的稳健设计,这也是最容易从经典设计延伸出来的稳健设计方法。2023-5-2
田口哲学:

稳健设计:重要的不是100%符合规格要求(如下图的San Diego生产产品,是均值思维),而是产品指标偏离目标值的程度(变异,可变性降低,这是变异思维)。
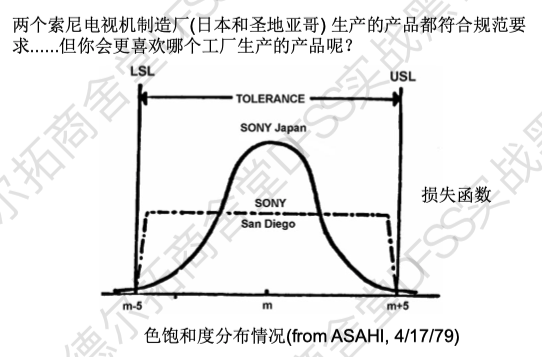
稳健设计的目标
- 理想化功能:稳健设计的终极目标是理想化功能,即不受噪声变量的影响。
- 噪声策略:通过研究噪声因子,使产品对噪声变量不敏感。
- 2步优化:先达到目标,再想办法降低变异。如果一开始就能梳理清楚都有哪些噪声变量,也可以直接将噪声变量作为x研究,类似于后面要讲的”偏导数法“。

三种稳健设计方法及比较; 乘积表法更简单(样品设计阶段),但只考虑主效应;组合表法和多重响应法需要更多的统计技能,可以分析高阶项;能够精确控制噪声因子时可以用组合表法(试产,中试设备等),不然就用多重响应法(批量生产,规模生产);三种方法适用于不同的开发阶段。
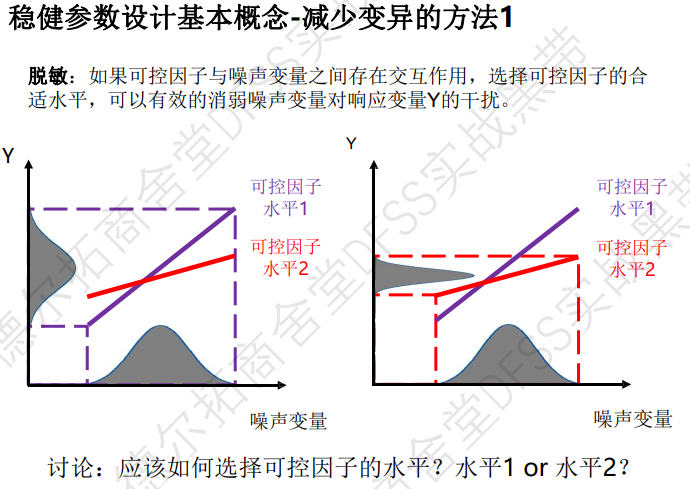
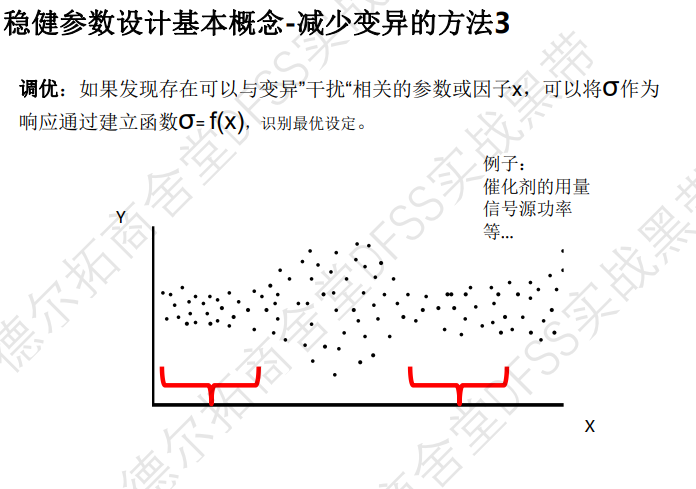
稳健参数设计——减少变异的方法:
方法1——脱敏:寻找具有交互作用的可控因子和噪声变量,在特定的可控因子水平下,噪声变量对响应波动更小。(下图所示,噪声变量对于较宽的响应范围,而可控因子与噪声变量具有交互作用,在水平2的情况下,响应的波动范围更小,所以选择水平2,来降低噪声变量的干扰。)
方法2:缓化,如果噪声因子对响应变量的影响是非线性的,并且可以设定噪声因子的水平,就选择干扰最小的设定范围。(方法1是一个噪声变量的波动范围,通过设定可控因子的水平来控制干扰; 方法2是噪声变量有很多可选的范围,寻找一个干扰更小的噪声变量的范围】

方法3:调优,使用一个控制参数,调整噪声因子。(意思是,更细致的研究噪声变量的来源,将噪声变量作为一个响应,寻找更精确的设定条件,缩小噪声变量的波动范围)
稳健设计—噪声变量的分类

- 固定设置参数的变化,设定参数并不能完全保持不变。比如UV光强设定5mW,实际因为衰减和不定期更换有变化,比如设定电压有波动,比如化学品原料纯度有波动等等。
- 实际值和名义值的差异,这种属于内噪音(internal noise),比如很多参数都在正负10%范围内波动。
- 环境的变化,使用条件和环境条件的波动称为”外噪音“(external noise),包括温度、湿度、洁净度、震动、空气流动(之前的纸牌试验),等等。
- 载荷因子,正常工作条件下因为实际使用存在的差异,有点像操作人员带来的个体之间的差异,比如纸牌降落试验中的人员身高
- 产品内部差异,空间差异,时间差异:比如涂布线上横向和纵向的UV光强差异,刚开机和充分预热后的差异。
- 损耗降级:随时间的一个衰减性因素。
稳健设计的过程和步骤–基于田口方法
田口实验设计,内表设置可控因子,外表设置噪声变量; 试验次数较多,这样可以排除内标因子和外表噪声之间的交互作用。
响应变量是信噪比S/N,而且是望大,即信噪比越大越好。
使用信噪比优化和衡量产品或过程的稳健性。
信噪比是一种特殊的响应变量,在噪声存在的情况下衡量性能,将可控因子和噪声因子的互相作用定量化。
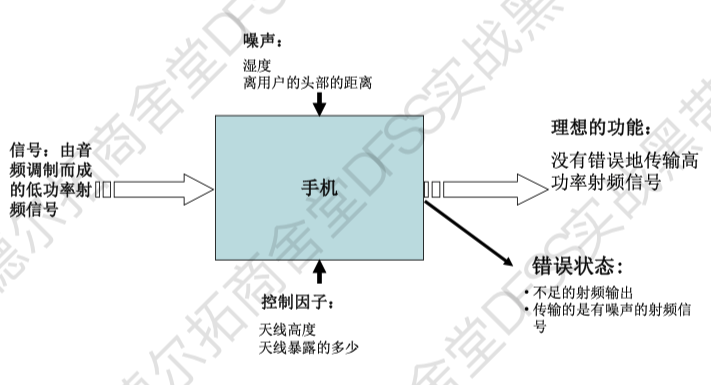
参数图(P-图),明确工程系统的控制因子、噪声因子、响应变量
控制图,输入,输出(期望结果,不期望结果),控制(可控因子,噪声因子)。 比如纸牌试验中,使用参数图明确系统的细节。然后再进行试验安排、收集数据、分析数据。
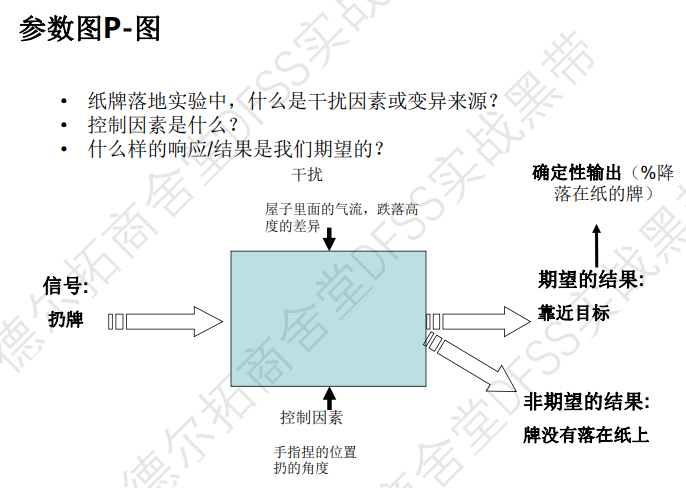
案例练习: 纸牌案例
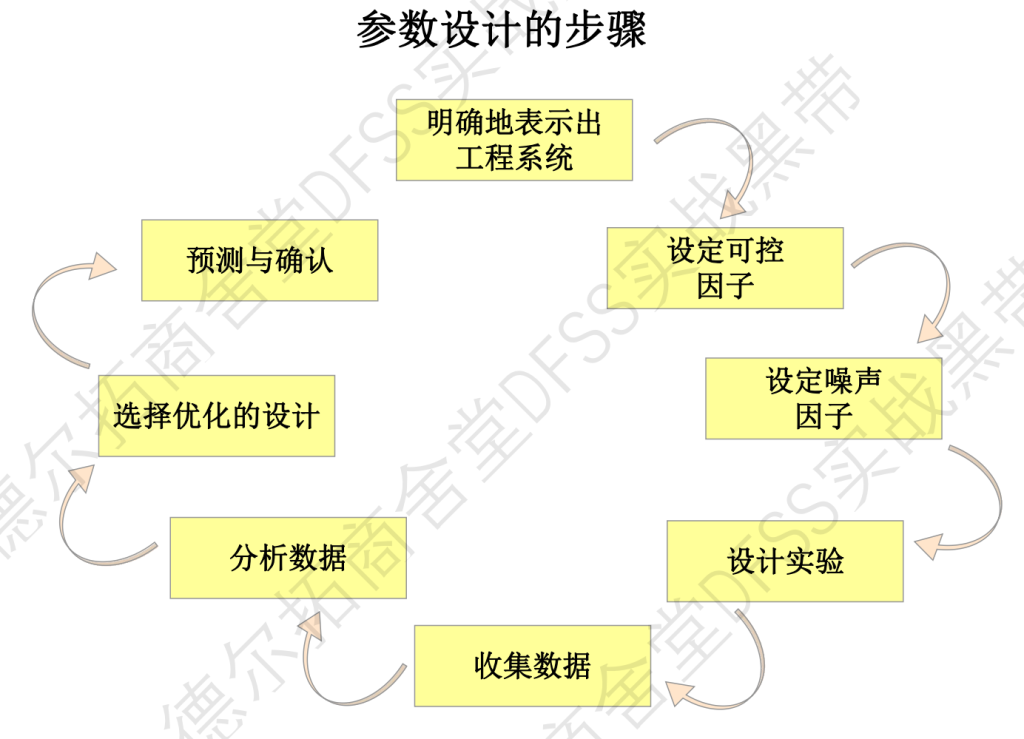
田口稳健设计的步骤:
- 明确地表示出工程系统,确定可控因子和噪声变量 (使用参数图P-图)
- 根据可控因子-分配内表,选择L4正交表(两因子两水平)
- 根据噪声变量-分配外表,这里一共有两个噪声因子,同样是L4正交表,竖排变成横排作为外正交表。
- 实验
- 数据收集 (每个条件只重复一次?)
- 分析数据——均值,方差,信噪比,方差分析,因子效应
- 选择最优设计,优化的量化指标是信噪比最大化,信噪比反映了噪声变量对系统变异性的影响。
- 预测和确认,根据预测的最佳设置,进行实验确认。
| 手指位置 | 跌落方向 | 弱风和低 | 弱风和高 | 强风和低 | 强风和高 |
| 窄 | 垂直 | 19 | 25 | 28 | 20 |
| 窄 | 水平 | 18 | 20 | 22 | 24 |
| 宽 | 垂直 | 30 | 19 | 27 | 33 |
| 宽 | 水平 | 12 | 15 | 14 | 17 |

补充介绍:Excel 规划求解器是什么,为什么要从Minitab上跳出来用excel规划求解器,为什么Minitab给不出最优的噪声变量参数?
ChatGPT:Excel 规划求解器是 Microsoft Excel 内置的一个工具,用于解决各种优化问题。它基于规划求解算法,能够处理线性规划、整数规划、非线性规划等各种类型的优化问题。通过使用 Excel 规划求解器,用户可以定义问题的目标函数、约束条件和决策变量,然后求解器会尝试找到满足约束条件并使目标函数最优化的解。这对于诸如资源分配、生产计划、项目管理等问题的优化是非常有用的工具。Excel 规划求解器的使用方式相对简单,但对于复杂的问题,可能需要一定的规划和算法知识来正确地建模和求解。
第32讲:田口稳健设计实战
备注:稳健设计的关键是参数分析,明确输入、输出(响应变量),可控因子,噪声因子,可以用一个黑箱子(p图)描述。
案例1:手机总辐射功率(staticTRP1),内表是L16正交表(两因子四水平共16次实验),外表共5+2个条件。
案例2: 乘积表(静态)(DOE-15田口)
案例3: 乘积表(动态)(DOE-16数据文件)
第33讲:马氏田口——放弃
2023-5-2 回顾第31讲资料,快速过第32讲,还需要用软件练习书中的案例。2023-5-13 再次回顾第31讲,done; 2024-4-5 回顾笔记;
4.3 经典DOE序贯设计 (第34-39讲) 单独整理
4.4 稳健设计-蒙哥马利组合表法 (第40-41讲)
组合表法的核心就是偏导数,首先构建响应变量的回归方程,然后对噪声变量求导,导数会与可控变量有关,选择导数为零的可控因子的取值。
根据因子数确定试验次数,具体用全析因还是部分析因,根据解析度,确定分析到二交互甚至三交互,一般是用解析度=V,这样就可以保留二交互;也可以使用部分生成元法,进一步降低试验次数。
组合表法中的稳健原理是”对噪声脱敏“,而脱敏的核心是找到噪声因子和哪个可控因子有交互作用,然后选择使对噪声因子求导为零的可控因子设定。
这样就更好理解三种稳健设计的方法对比了,感觉组合表法(偏导数法)是最好用的方法,本身很像部分析因设计,而且噪声因子本身也是作为因子X使用。 ——2023-5-10
听完第三种稳健设计(多重响应法),就知道组合表法有很明显的局限性,首先要将噪声因子作为x变量构建实验设计,会增加试验次数;其次要有噪声因子和控制因子的交互作用;另外有时候还要用excel规划求解工具(why)。 —— 2023-5-25
2023-5-10 直播,组合表法第二部分
案例1:组合表法机加工案例(多噪声因子 )
响应变量:
可控因子:
噪声因子:生产线无法精确控制,存在较大变异;而在实验室可以控制噪声因子来研究噪声因子对响应变量的影响。
试验:5因子,进行部分因子16次试验,加上四个中心点,总共20次实验。
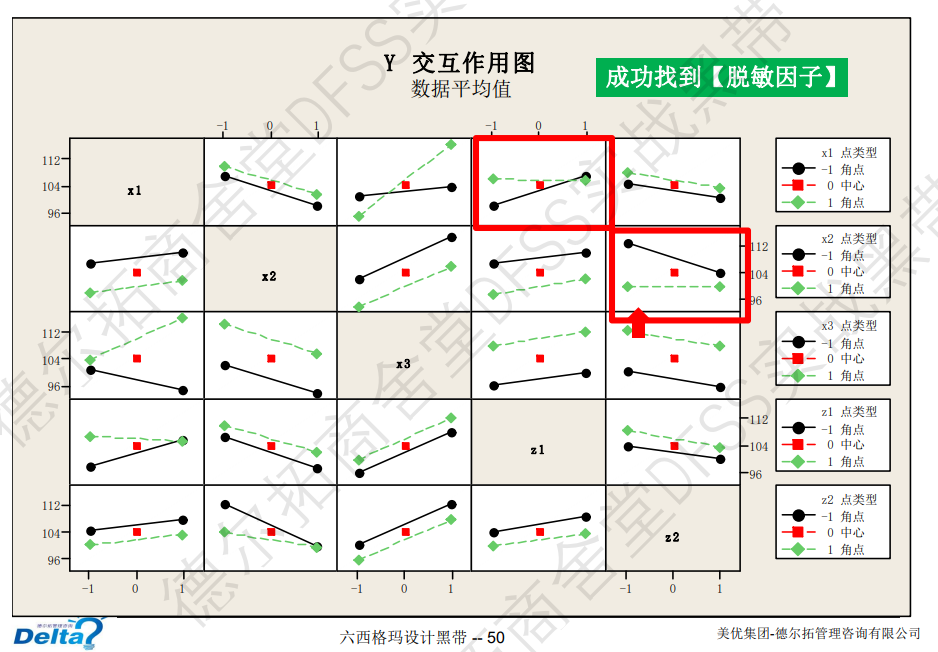
关键点:研究Y交互作用图,查看可控因子(X1,X2)和噪声因子(z1,z2)之间是否有交互作用,如下图所示的x1和z1,x2与z2之间有交互作用,一方面从机理上解释,另一方面这就是稳健设计的突破口!
找到可控因子和噪声因子之间的交互作用,也就找到了【脱敏因子】
写出代码化的回归方程,然后分别对两个噪声因子求偏导数,使偏导数=0,也就是回归方程对该噪声因子的影响最小。

使用【响应优化器】进行优化设计,可以查看调整z1和z2时的响应变化程度。
回归函数,可以分解为均值模型+方差模型,
规划器求解:使用excel的规划求解功能(规划求解加载项),原理就是用excel来构建回归函数,输入回归函数的不同变量(模型系数,误差方差等来自于minitab ),
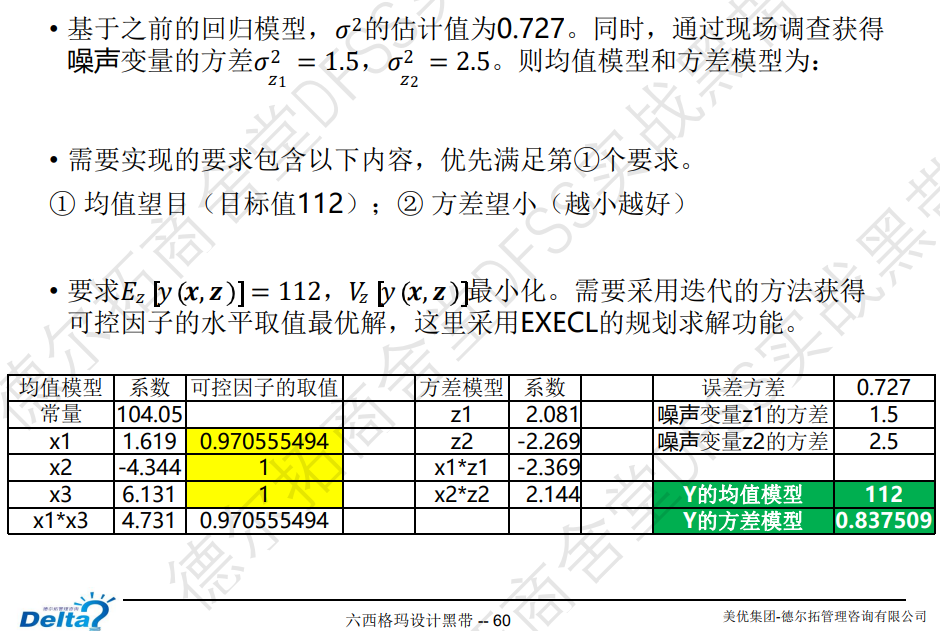
为什么用minitab求解,y的变异会大很多 ?
备注:
图形化汇总:响应变量的范围,是否覆盖了我们想要的目标值。
第一次“分析因子设计”时,先不勾选中心点,只计算主效应和交互作用,避免中心点干扰主效应和交互作用(效应只用两个端点数据来计算);只有当发现有显著的弯曲时,或者说要计算回归方程时,才需要用中心点。 所以经典DOE的九步法中都不用中心点,等到需要计算误差时,计算回归函数时,才需要中心点。
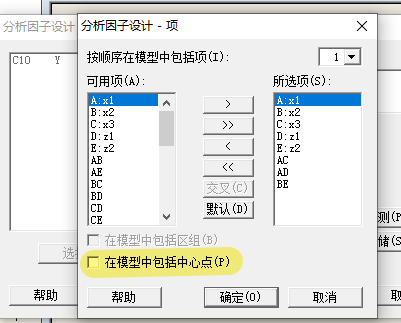
数据是否有异常点,
组合表法案例:低频信号
6个变量(3可控+3噪声),使用分辨率=V的部分析因设计(放弃三交互),一共32次试验,再使用指定生成元法(指定需要考虑的二交互作用,根据现实工作经验来解释,明确某些交互作用不可能出现而删除),进一步减少试验次数。
噪声因子F和可控因子之间的交互作用都是不显著的,所以噪声因子F无法被脱敏。
同样是得到回归曲线,对噪声因子求偏导数,选择偏导数为零时得可控因子的设定值,可以得到y=30时的设定值。
如果设定y=28,无法用优化器计算,为什么? 需要用规划求解器计算。
4.4 稳健设计-组合表法 (第42,43讲)
2023年5月14日周日直播
第42讲 稳健设计 组合表法(静态,非线性情况 –> 缓化方法)
备注:上一讲是使用脱敏方法寻找最后的噪声因子的变量,通过经典DOE设计,将噪声因子作为x,发现噪声因子和可控因子之间的相互作用,获得回归方程,对噪声变量求偏导数,使偏导数=0,计算出可控因子的参数,此时就是噪声因子对响应的干扰最弱的参数设定。
备注:如第31讲稳健设计基础所述,稳健设计有三种方法,除了脱敏,还有缓化和调优方法。 第43讲的案例就是使用”缓化“方法,因为不存在噪声因子和可控因子的交互作用,但是回归方程中有噪声因子的平方项,也就是响应对噪声变量有弯曲。 为了研究弯曲,就需要增加试验数据,构建响应曲面设计,比如CCC设计。使用RSM的回归曲线,得到响应和噪声的二阶模型,然后再求导,将偏导数为零,计算出对应的参数设定。
备注3: 稳健设计的一个特点是,需要手动计算偏导数及其为零时的参数设定,然后再回到minitab上使用响应器工具。
备注4:为什么叫组合表法,不直接叫偏导数法? 不论是脱敏还是缓化,核心都是获得回归方程之后对噪声变量求偏导数,然后计算偏导数为零下的参数组合?
备注4: 给出了回归曲线之后,如何选定最优的参数设定:(1)minitab的响应优化器,需要手动调节,(2)excel的规划器求解;(3)Minitab的响应优化器,只能给出平均值最优的参数,需要输入自己设定的取值; 既要看实际需求,某些参数要考虑价格等实际情况。
组合表法:要求噪声因子可控,使用均值的回归方程进行偏导数法估计误差,需要存在能使用脱敏、缓化的交互作用和弯曲情况才行。
理想状态:目标对准中心,波动越小越好。
问题:哪些情况需要用Excel规划求解?
第42讲: 张望梅老师分享两个案例,一个是没有交互作用没有弯曲的案例,一个是同时存在交互作用和弯曲的案例。
案例1: 化学熔点。不存在交互作用,存在弯曲,使用”缓化“策略,直接在minitab中用响应优化器,结合偏导数为零的计算结果即可,不需要用excel”规划求解“功能。
案例2: 组合表法电机功率。既存在噪声因子和可控因子的交互作用,又存在噪声因子的弯曲。
最难的部分还是”规划求解“部分,我自己并没有弄清楚原理,自己做不了,还需要研究细节。
课件最后部分介绍了原理情况:
噪声因子要区分成是否可调
f(x):可控因子
g(x, zj): 可调噪声变量zj,以及可控因子与可调噪声变量的交互作用
h(x, zi):不可调的噪声变量zi,以及包括Zi的交互作用。
方差模型= (偏导数)^2 * 噪声变量的方差


第43讲 组合表法+规划求解的复杂应用

案例:组合表法精密量具(动态模型)
Minitab响应器只给出了均值达到要求的参数设定,而不考虑噪声处于干扰最小的设定值,也不考虑响应的波动大小。 此时就需要使用规划求解,同时考虑均值方程和变异方程。
4.4 稳健设计–多重响应法(第44,45,46讲)
最常用的稳健设计方法是多重响应法; 对于组合表法,需要非常清楚噪声因子的来源并作为x进行控制。
第44讲,介绍响应曲面分析(RSM),包括为什么做RSM,三种常见的中心复合设计,中心点实验,区组化;
2023-5-24 第45讲,串讲知识和实战分享;欧老师先补讲第44讲没有讲完的部分。
关键点:正交区组化,中心复合(不要随便改中心点,不然软件就变成了回归分析)
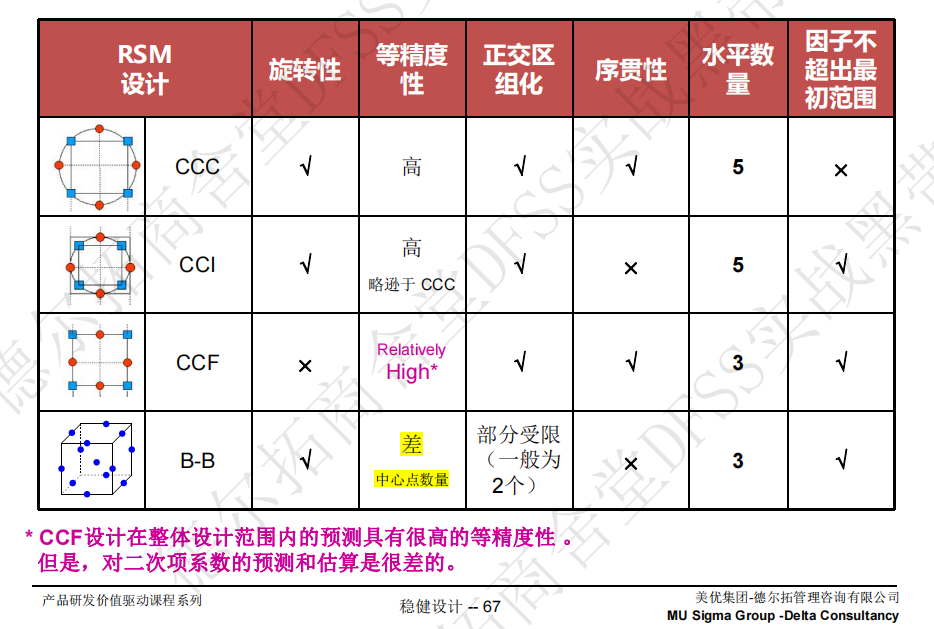
强调:现在主流的DOE都是序贯设计,序贯设计都是以经典DOE为基础;序贯设计突破点性境界是RSM,使用中心复合试验,通过增加轴点试验,联合之前已经完成的实验点,组成更完整的数据点,可以分析非线性的场景。
RSM强调旋转性和等精度性,最好是在一个球面上构建实验点(CCC,CCI,B-B,球面=旋转性)。
涉及到响应曲面分析时 ,中心点实验非常重要,涉及到误差评估。
CCC:唯一的缺点就是“因子超出最初范围”,如果原来的-1和+1已经是最大范围,那就没办法向外扩展,只能用CCI等向内扩展。
正交区组化:区组本身可以作为一个因子去研究,特别是不好调整和不方便控制的因子(类似于Design expert中的HTC 因子)
案例:Elasticity与三个因子之间的关系
一开始是经典DOE数据,发现R-sq预测=0,R-sq调整=44%很低,发现是线性拟合存在弯曲curvature,p=0.002。
此时就应该继续补充实验点,包括中心点和轴点,从线性模型转化成非线性拟合,即RSM design。
增加轴点实验,这是第二个区组要增加的实验点,所以序贯设计中的两次实验就是两个区组化!
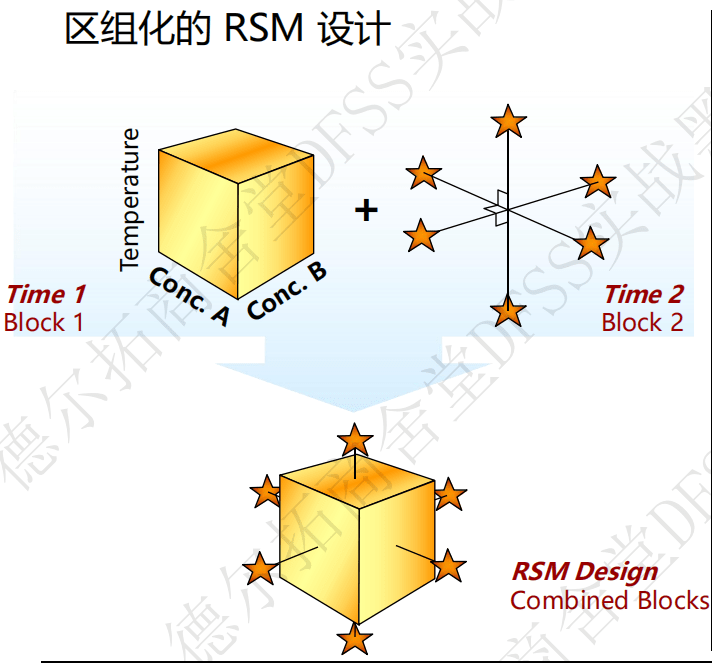
问题:DX中如何进行RSM?
案例分享:如何使用区组化研究噪声因子——蓝膜问题
研发人员大都是没有方法论的,还很傲慢;黑带与技术沟通所有的控制因子和变量,发现一个潜在的胶水包装材料(红膜,蓝膜),使用区组化进行评估;最后发现区组显著,即蓝膜和红膜不一样。用蓝膜包装的silicone adhesive,和红膜包装的silicone adhesive不一样。
第45讲 多重响应法 2023-5-24
要准确估算模型的误差项,一个办法是增加重复实验;
Box方法:
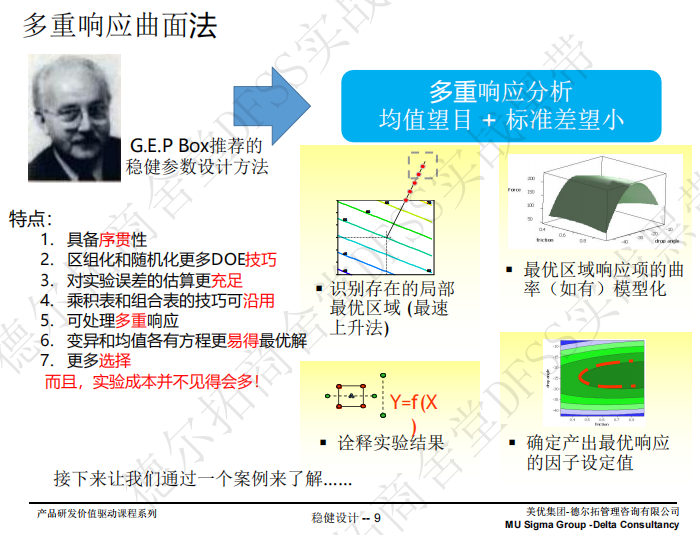
案例:V型螺栓产品,两个x,一个y,响应望目,已经找到预期的均值;但是不知道有什么噪声因子,应该如何做稳健设计?答案是田口或多重响应法,除了正常的作业条件,增加一组“更差的作业条件”和“更好的作业条件”,人为的选择更小波动和更大波动的操作条件,相当于进行了三列重复性测试,(三个测试条件相当于三个田口设计的噪声因子)
多重响应:至少有两个y
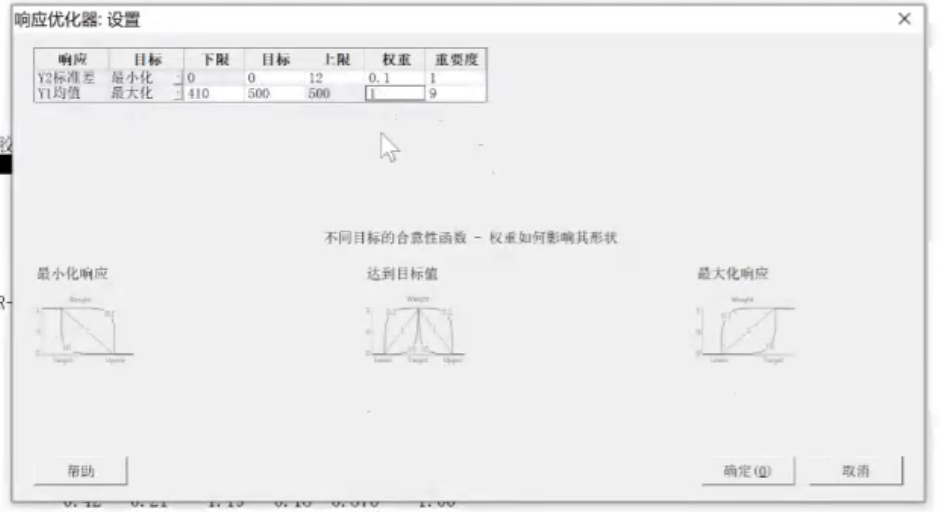
关键词:【合意性】【权重】【重要度】
【权重】: 即响应达成目标值的重要性,还是只需要超过下限即可;取值范围0.1到10,默认选1,数值选10时,快速逼近目标值; 针对单一响应
【重要性】:有多个y时,综合考虑多个y的合意度和权重,给出一个汇总的合意度。
4.5 容差设计 单独整理
2024-4-5 快速过完去年整理好的草稿,多重响应法和组合表法的内容,我以后再重读更新,博文中并没有整理好;最常用的是多重响应法,但是我这一块居然没有整理哎。