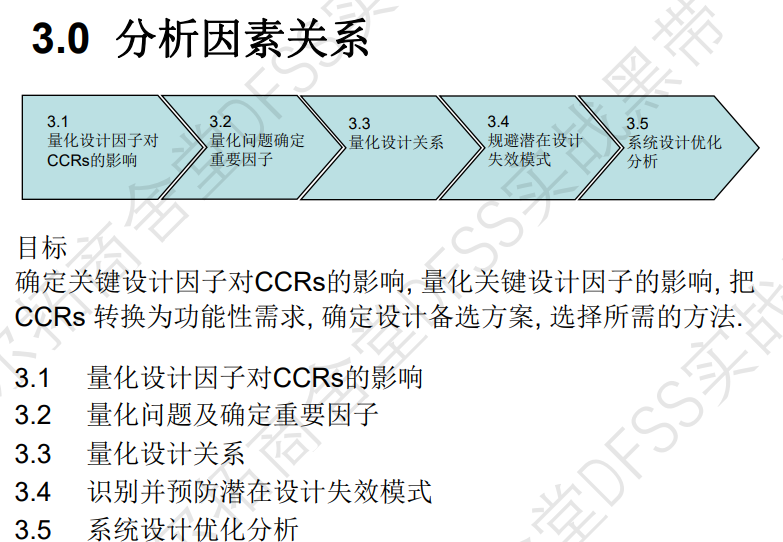
分析阶段part 1, 包括3.1 和 3.2, 其中3.1是量化CCR和关键设计因子的关系(核心是CTQ流下树&能力流上树),3.2是量化问题及确定重要因子(核心工具就是比较,分析的本质是比较,假设检验是一种高级的比较工具)
分析阶段par 2,包括3.3 量化设计关系(使用的工具是相关性分析和回归分析),3.4设计FMEA,3.5 系统设计优化分析(工具是TRIZ和普氏矩阵)
关键知识点:
- 相关性分析的基础知识,
- 模型分析的具体细节
- 残差分析的具体细节,如何分析四合一残差图
结合工作练习:
- 简单线性回归:比如响应为胶带的T380或T405,变量为吸收剂的含量取对数(因为x和y是指数power曲线),然后用minitab进行回归分析。
3.3 量化设计关系 (第23,24讲)
本讲介绍相关性和回归分析的基础知识(散点图,相关性系数等),一元线性回归分析(模型分析,SS,MS,F,p,S,R-sq,R-sq(adj),DF,SSe; 四合一残差图;残差分析);多元线性回归,多项式回归。
关键是基础知识和一元线性回归的模型分析和残差分析,后面会经常用到。
基础知识
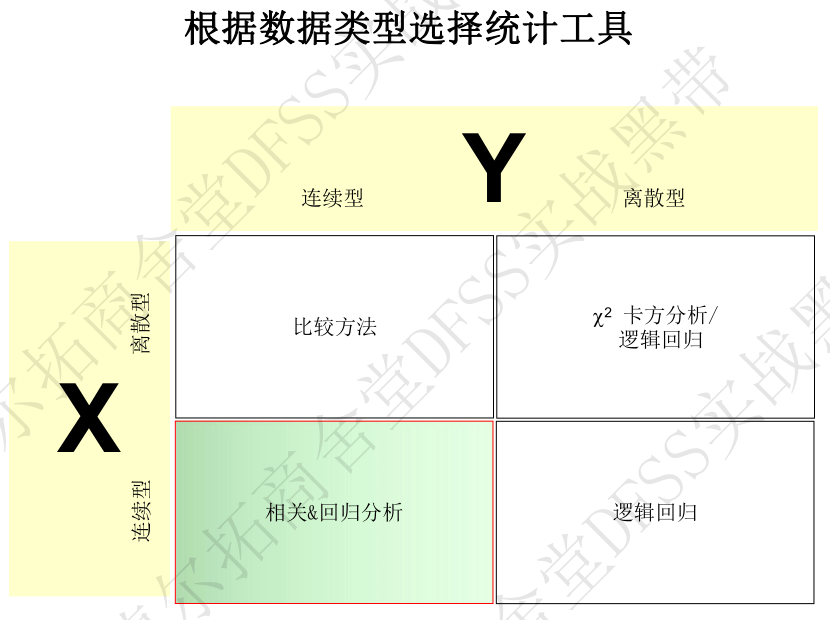
- 回归分析针对”连续变量x和连续型响应y“之间的相关性分析,可以建立传递函数(方程式,数学模型)
- x和y存在显著性相关的假设检验:
- x和y之间的相关性大小:查看模型的系数
- 多个x的priority分析:系数大小排序
- 稳健性分析:使y对特定的噪声变量x脱敏,分析导数最小或为零的变量设定。
- 相关并不代表因果,还需要结合“专业知识和经验”给出理论分析。(《原因与结果的经济学》也讲这个,小心互为因果、小心单纯的先后发生等情况;还有一个情况是“斯德哥尔摩股票经纪人”案例,只看到局部数据就会被蒙骗。)
- 定性和可视化的相关性分析:散点图
- 定量化描述两个变量x和y之间的相关性:相关性系数,计算公式如下,r=1是绝对正相关,r=0是完全不相干,r==-1是绝对负相关。
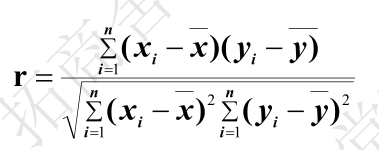
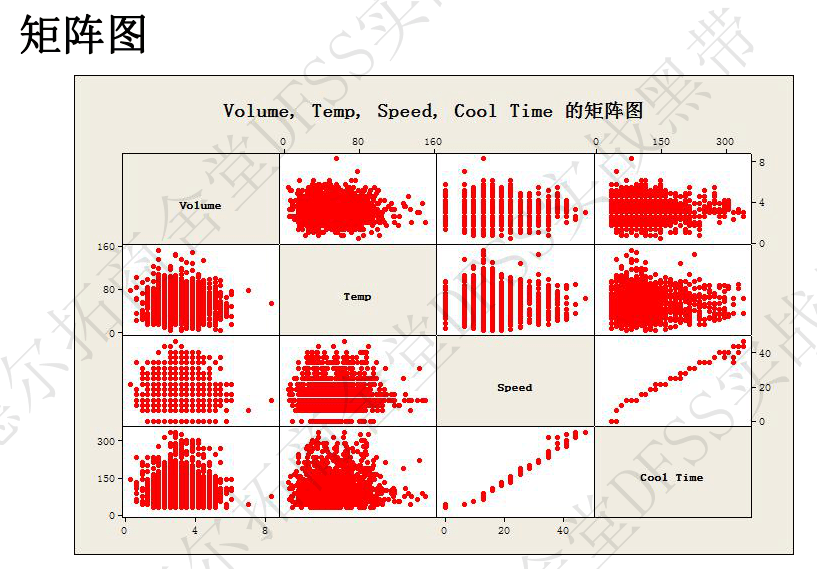
- 实操:有很多组变量,先看矩阵图(两两之间,定性观察),然后用“统计——基本统计量——相关”进行两个变量之间的相关性确认。矩阵图如下:
简单(一元)线性回归分析:
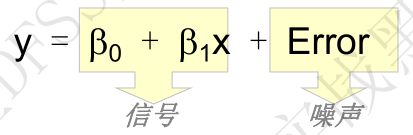
- 一元:只有一个x,即单因子方程式; 线性:只考虑变量x,不考虑x的平方项和高阶项。
- 如何根据数据点(x1,y1),(x2,y2),(x3,y3)…计算出上面方程式的截距、斜率、噪声(误差项): 答案是”最小二乘法“,确保”观测值和模型预测值的差值(即误差)的平方和之和最小”,也就是SSe最小,建立拟合线,即“最小二乘回归线”。斜率和截距,直接用软件给出即可,也有计算公式,略。
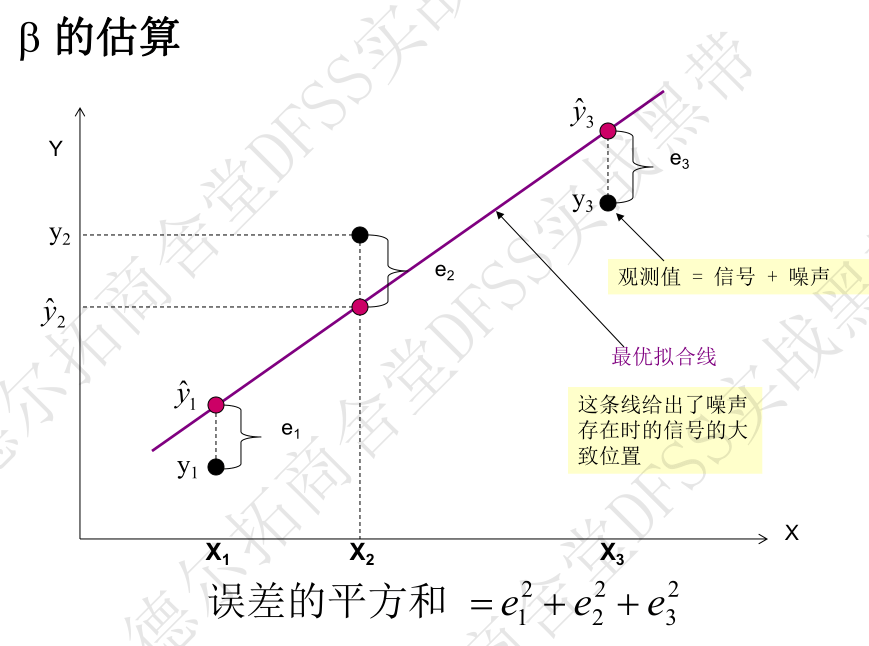
- minitab练习:“统计——回归——拟合线图”,选择线性、二次或立方回归模型,针对只有一个变量x的情况,否则就要用”统计——回归——回归“
- 拟合线图的S,R-sq,R-Sq(adj)的含义,如下图:
- S:即RMS Error(误差均方根),是模型误差项的标准差,等于模型“误差项均方”的平方根。
- R-Sq, 即R平方,反映用模型来解释的总变异的比例,比如R-Sq=98%,代表总变异的98%可以用这个模型来解释。
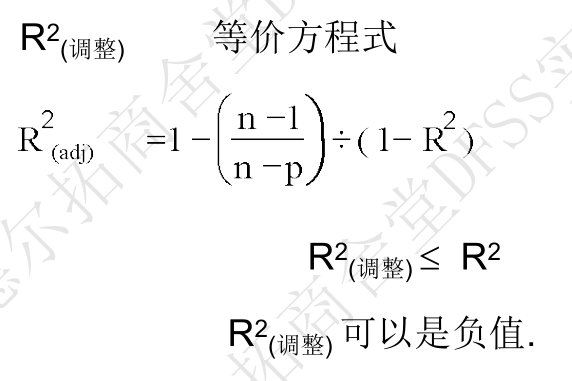
- R-Sq(adj):当有很多变量时,平方项SS会变大,一些相关性不显著的变量会放大R-Sq(因为要计算所有变量的误差平方项);为了排除变量数量过多的干扰,使用MS(均方=SS/自由度)替代SS,重新计算R-Sq。
- R-sq和R-sq(adj)的接近度,反映了模型到底有多好。如果差异太大,说明混入了太多的不相关的变量。
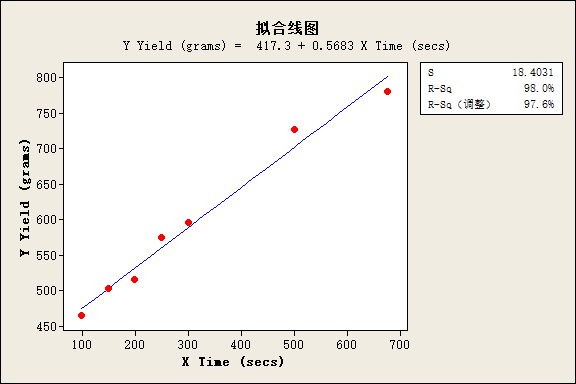





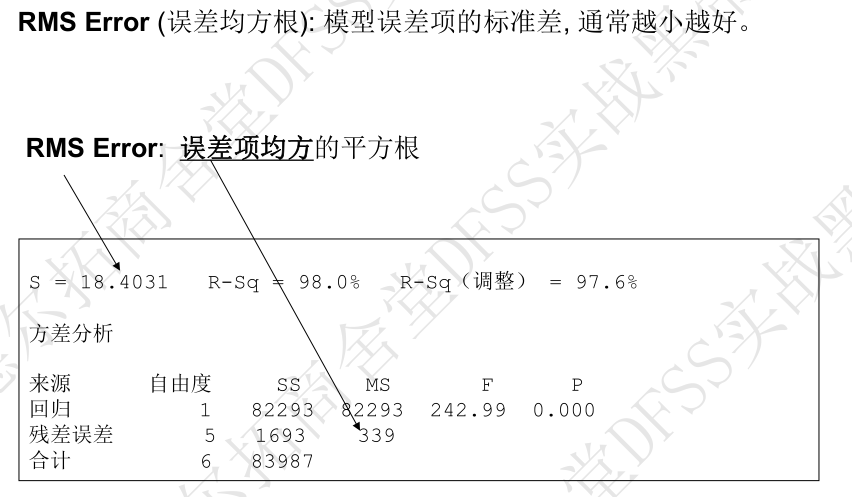
- minitab导出拟合线图、回归拟合结果中的参数含义:
- S,R-sq, R-sq(adj) see above
- 方差来源:回归模型、误差、合计。 SS total) = SS(model) + SS(Error)
- 自由度DF:回归自由度(包含截距的模型项数p-1),误差自由度(n-p),总自由度(数据点n-1),DF(total) = DF(model)+DF(error), n-1 = p-1 + n-p
- 平方和SS:均方
- 均方MS:
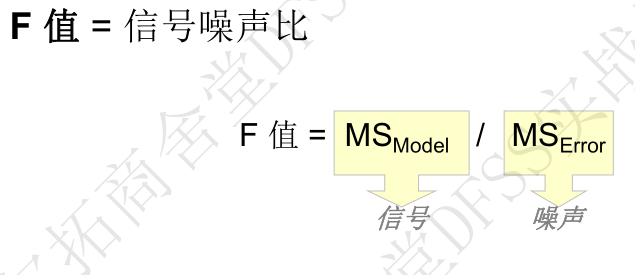
- F检验: 模型方差SS(model)和误差SS(Error)之间的比较, 即信号和噪声之间的比较,零假设为“模型不显著”,即y和x之间没有相关性,总平方和SS主要来自于SS(error)
- p: 假设检验,p<0.05,拒绝原假设(模型不显著),说明y和x之间存在显著的相关性。

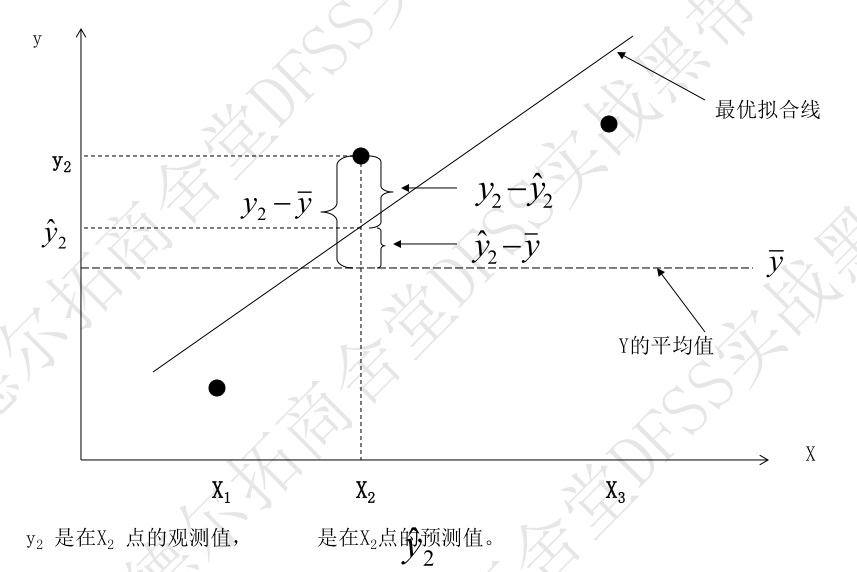




残差分析
- 以上是模型的误差分析,如果模型很好,误差SSe会很小,F检验显著。
- 更进一步分析模型的好坏,就需要分析“残差”,即单点的检测值和预测值的误差情况。
- 使用模型前,一定要使用残差分析进一步检验模型是否正确。在回归-拟合线图,方差分析,DOE等分析中都会用到残差分析。
- 具体的残差分析方法:(1)参考的分布,(2) 后面涉及到的四合一图,就是更细致的残差分析方法。
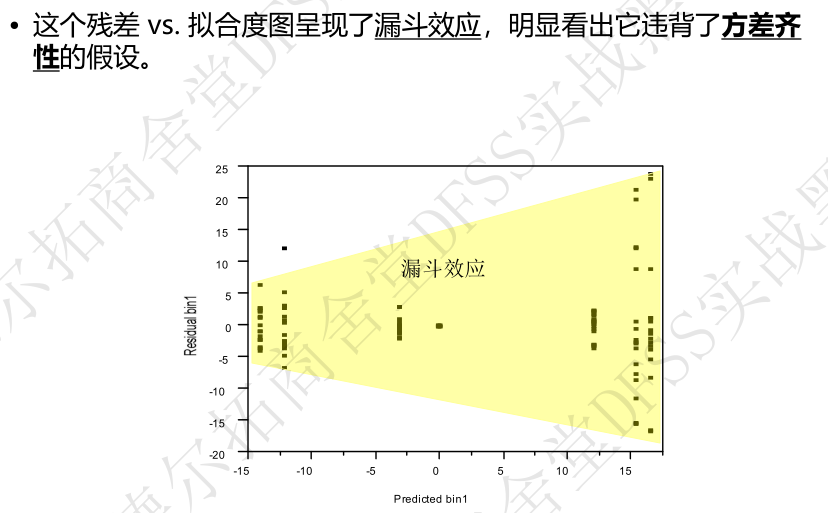
- 分析残差有助于我们分析拟合模型的潜在问题:(1)违反了模型假设,(2)失拟,(3)异常值。
- 模型充足性——失拟(lack of fit,lof):多次重复的观察值的均值和预测值之间的差异。Lack of Fit manifests bias or difference between the average of repeated observations and the predicted values.
- 四合一残差图: Residuals
- 1. 残差 vs 运行序 (时间顺序) —— 残差是时间独立的吗?
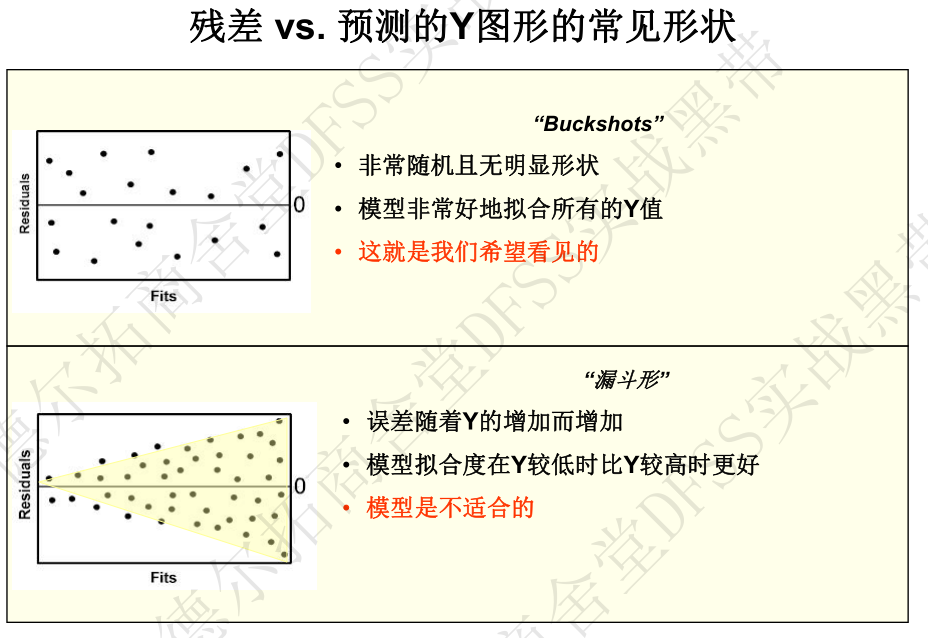
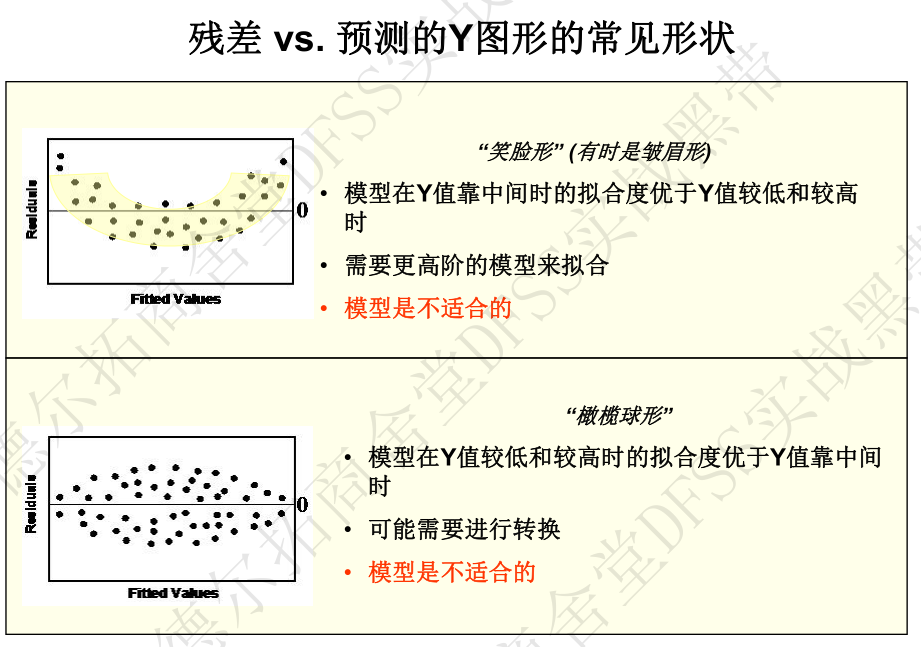
- 2. 残差 vs 预测响应值 (Residuals vs Fits)—— 残差是否随机分布在0附近,残差在不同的预测值上是否有相同的差异(方差齐性),是否存在失拟(残差图弯曲,即在某些区域,拟合值不能对应于重复测试的均值,而是对应到了偏大或偏小值,见下面失拟的定义。)
- 3. 残差的正态概率图 ——参考是正态分布吗,是否有异常值;
- 4. 残差图 vs X因子 ——是否存在异常值
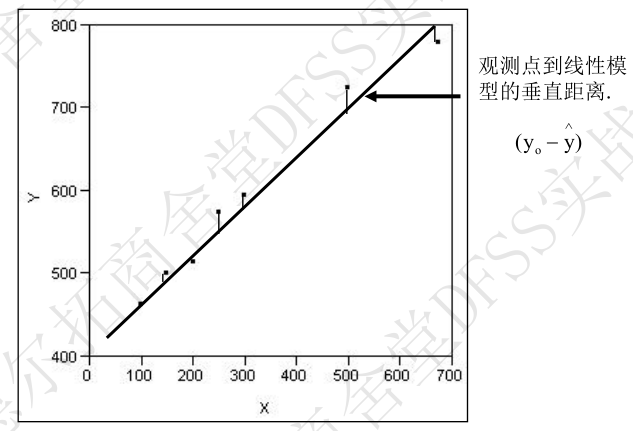



- 四合一残差图: Residuals
- 1. 残差 vs 运行序 (时间顺序) —— 残差是时间独立的吗?
- 2. 残差 vs 预测响应值 (Residuals vs Fits)—— 残差是否随机分布在0附近,残差在不同的预测值上是否有相同的差异(方差齐性),是否存在失拟(残差图弯曲,即在某些区域,拟合值不能对应于重复测试的均值,而是对应到了偏大或偏小值,见下面失拟的定义。)
- 3. 残差的正态概率图 ——参考是正态分布吗,是否有异常值;
- 4. 残差图 vs X因子 ——是否存在异常值
- 根据残差图,如果出现失拟、非正态(残差的差异不相等)、时间依赖、异常值等,需要考虑异常值的根源、正态转化、分析时间依赖性的原因等等。
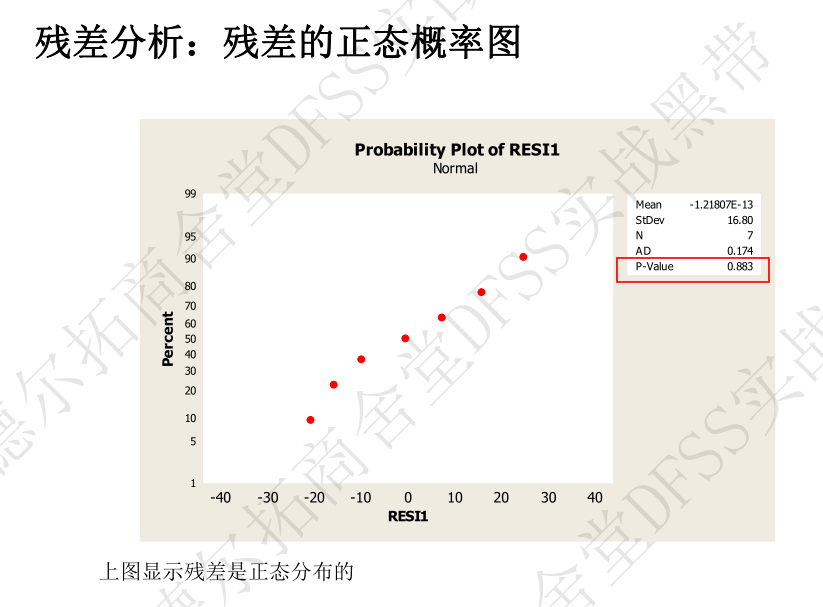
- Minitab计算,可以讲“残差”和“预测值”都储存在工作表中供进一步分析。比如使用“统计——基本统计量——正态性检验”分析计算出来的残差是否正态, P>0.05,无法拒绝原假设,残差是正态分布的。
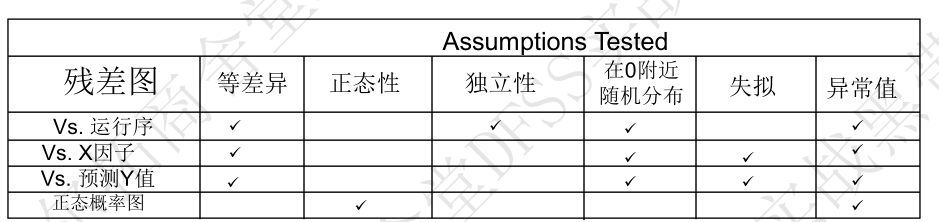

四合一残差图案例:
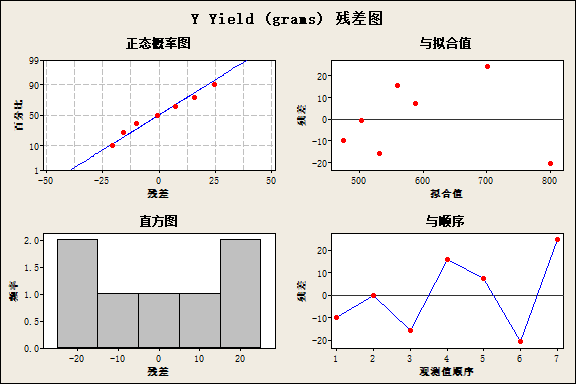
残差图 之 残差 vs 预测响应值
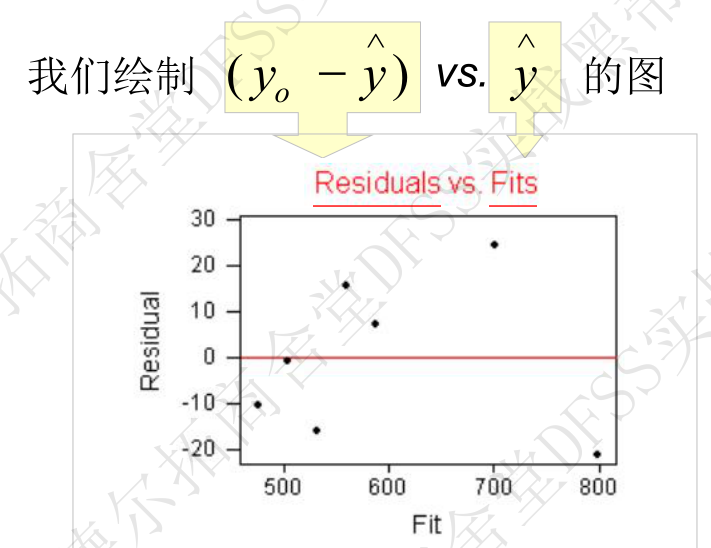


残差的正态概率图:p>0.05 (为什么是正态的??)
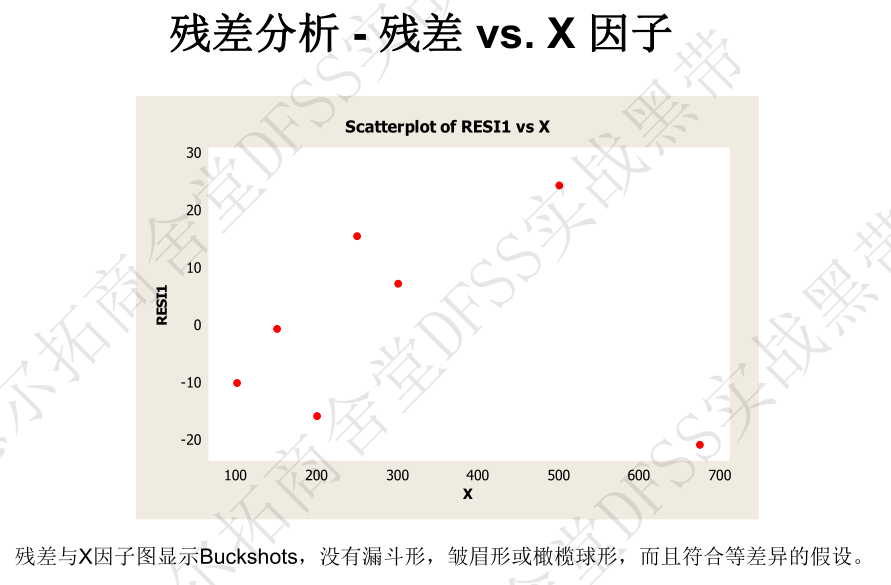

预测:
- 基于回归分析得到的模型/传递函数,预测特定变量条件下的响应,在90%或95%置信区间下,会落在什么范围中。
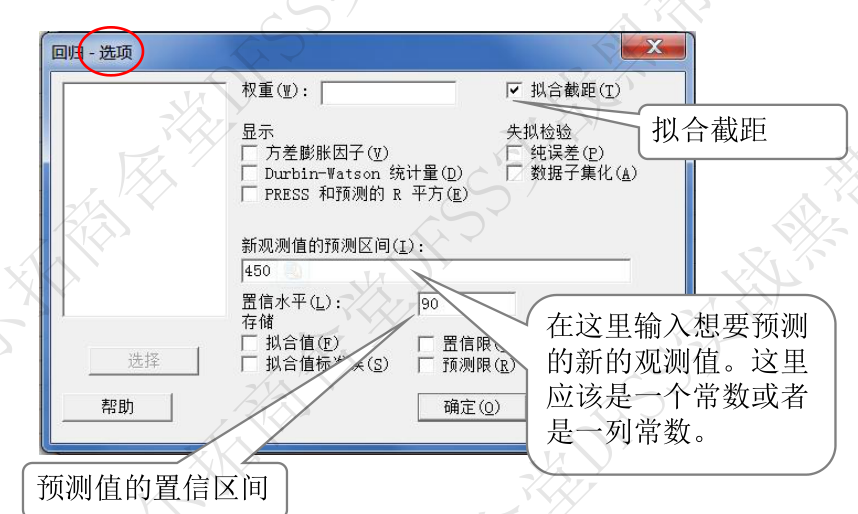
- 方法:回归- 选项,输入“新观察值的预测区间”和置信区间,如下所示。 【
下面的案例弄错了,新观测值是响应!不是变量x! 所以是基于回归方差和响应y,计算出需要设定的x的变量。】【上面理解错了,minitab的“新观测值的预测区间”,输入的就是变量x的设定值,然后计算出响应的预测值!!! 注意下面的450就是X time】 - 区分“90%置信区间”和“90%预测区间”,前者是当前实验条件下对该测试点的分析,后者是对未来试验的预测区间。
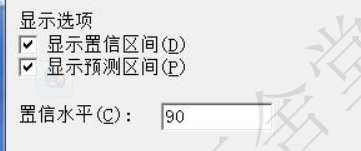
- 预测时,还有一种方法,是在“拟合线图“时,在”选项“中”显示置信区间“,”显示预测区间”,并输入“置信水平”, 这样就可以得到下图中包含置信区间和预测区间的拟合线图。 问题是,怎么量化出这些置信区间和预测区间?

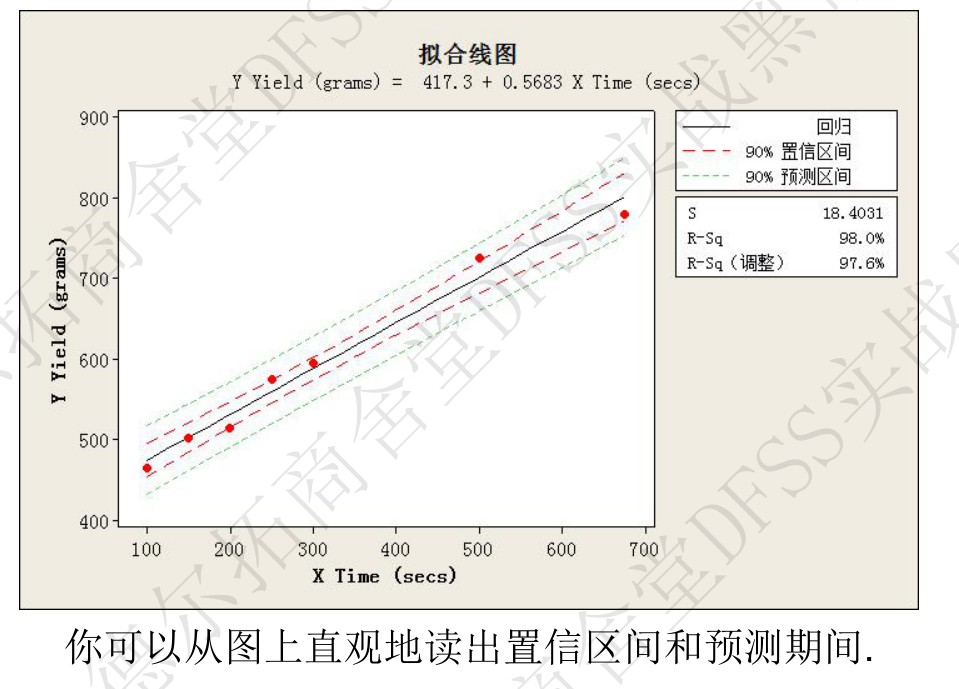
提醒:

案例练习:(有难度,我做错了,也想少了,特别是最后是要计算“下限值”。
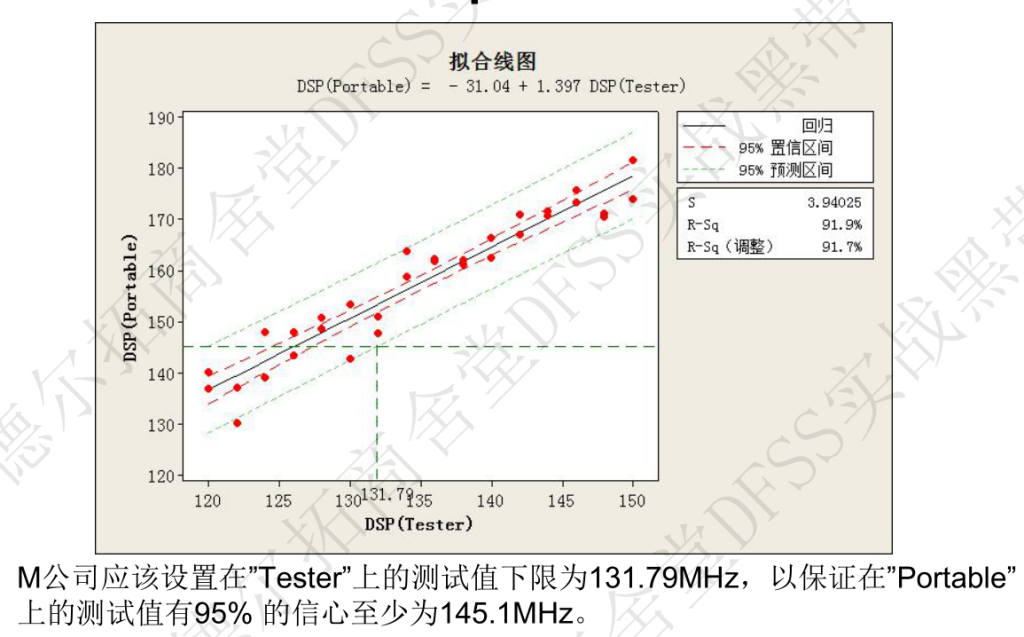
- 两种测试设备的结果之间的一致性对比,建立两个变量之间的回归方程,x变量(M公司)要求95%置信区间大于145.1,计算y变量(供应商)需要设定的下限;要建立回归方程,然后进行“预测分析“。
- 先用散点图看一下两组数据之间的相关性,相关性很强
- “基本统计量-相关”; pearson相关系数=0.959,强相关。
- “统计-回归-线性拟合”,将portable作为x,tester作为y;拟合,查看残差图,ok;拟合ok。查看S,R-sq,R-sq(adj)=91.7%,F,p=0. 说明模型显著,线性模型解释了91.7%以上的变异。
- “统计——回归——回归——选项“,输入新观测值145.1(portable=145.1)和置信区间95%。计算出tester的预测范围121.1-1325,那下限设定就应该是121.1
OMG,下面分析弄错了,x和y弄反了,因为portable观测值=145.1,这是对响应y的设定,而不是x的设定!!- 问题:我的方法计算出来的结果,为什么和老师的方法的结果不同;这两种方法是否不等价?需要后面再研究吧——2023-7-15


正确答案:
课件:并非是用test=145.1来计算portable,只是来说明portable=145.1时,tester应该会小于145.1, 老师是绘制了含有预测区间的拟合线图,然后大概推测预测区间下限=145.1时的x变量tester数据。 问题是,我的方法为什么不对呢? 直接用tester作为y,portable作为x,输入x的预测值=145.1

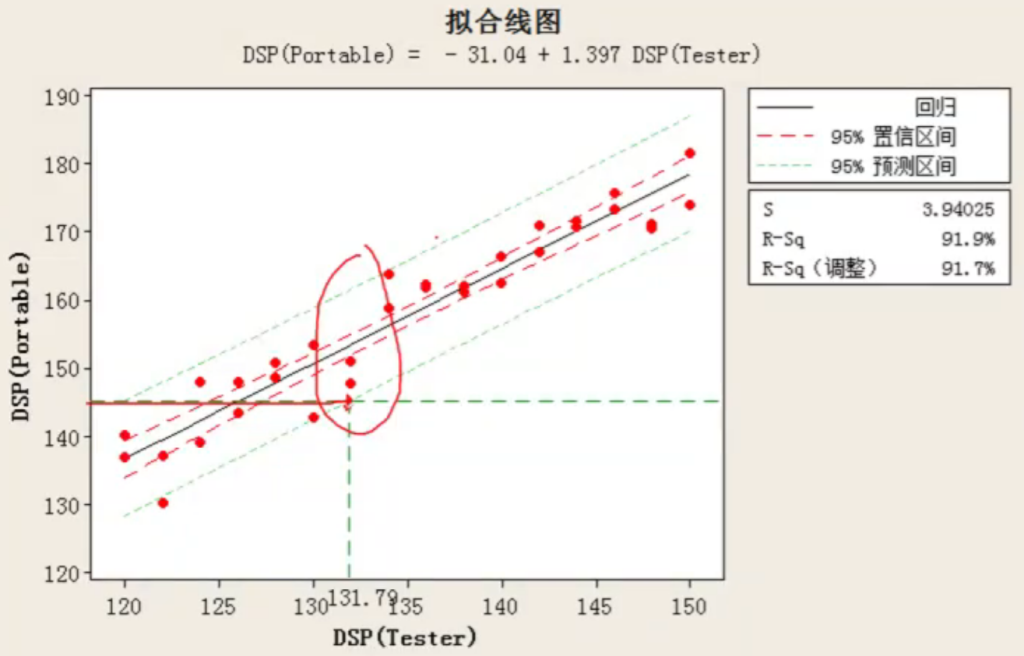
蒙特卡洛仿真+回归方差的结合案例:
我们知道了portable和tester的回归方程,下面再知道tester结果的分布情况,上面知道了portable=145.1时tester应该取的下限(132),然后计算这个下限在tester分布中对应的概率。这就是一个典型的参数检验问题啊。 至于用蒙特卡洛仿真,是不是把简单问题复杂化了?【我把问题弄简单了,实际上回归方程含有误差项,不能直接不考虑误差直接取其中的某一个值,放在分布中计算。——2023-7-15】
蒙特卡洛的高级之处是,可以结合回归方程和分布,计算出另外一个分布。

多元线性回归分析
- 多个连续型x变量和响应y之间的线性回归
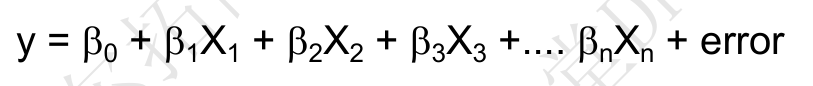
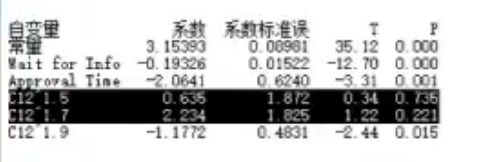
- 小心散点图的误导;因为散点图中没有相关性,但回归方程中却可能非常显著。 (为什么?)
- 回归方程的p<0.05,说明至少存在一个因子x显著影响响应y。
- 分析系数的p值,确认每个x是否显著;去掉不显著因子,重新拟合模型,直到所有的系数都显著。(DOE分析中,针对每个y,是否也可以删减x?,从而提高模型精确度?)
- 如果残差是非正态的,通常需要进行转换后,重新拟合。
多项式回归
- 涉及到x的二次项或高阶项,还有x之间的交互作用,比如x平方,x1*x2,x12*X2
- 什么时候用多项式回归?比如在线性回归中,观察预测值和x之间的关系,如果不是随机均匀分布,而是看起来像抛物线,可以考虑加上这个因子的平方项。比如minitab中手工加上几个高阶项,比如x的1.5次方,1.7次方,1.9次方等(那我为什么不直接把x取个对数,作为新的x呢,这样就变成了新的线性回归)
- minitab中加上几个新的列,比如平方项,立方项,作为新的变量x,再进行线性回归分析。
2023-7-15 周日,花了好几个小时重读完第23+24讲。
3.3 量化设计关系 广义线性模型 (第25讲) 暂略
彭咏天助讲
针对离散型回归分析,包括离散型x变量,离散型y的情况,速读,


3.4 规避潜在设计失效DFMEA (第26讲)
练习:学习附加资料的FEMA案例,和带公式的excel模版。
识别问题、描述问题、设计消除缺陷的解决方案。
关键内容:
- DFMEA的宏观流程图:框架,项目范围,p参数图,设计DFMEA12步骤
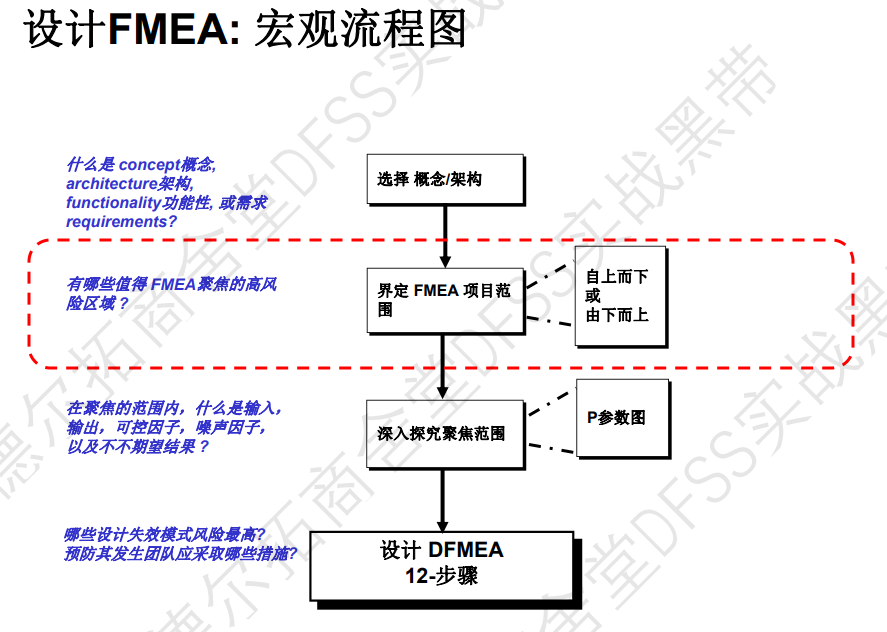
- 功能分析,功能树,
- 产品失效
- p参数图:定义参数涉及范围,联系输入和输出,识别和回顾设计参数、可控因子和噪声因子。
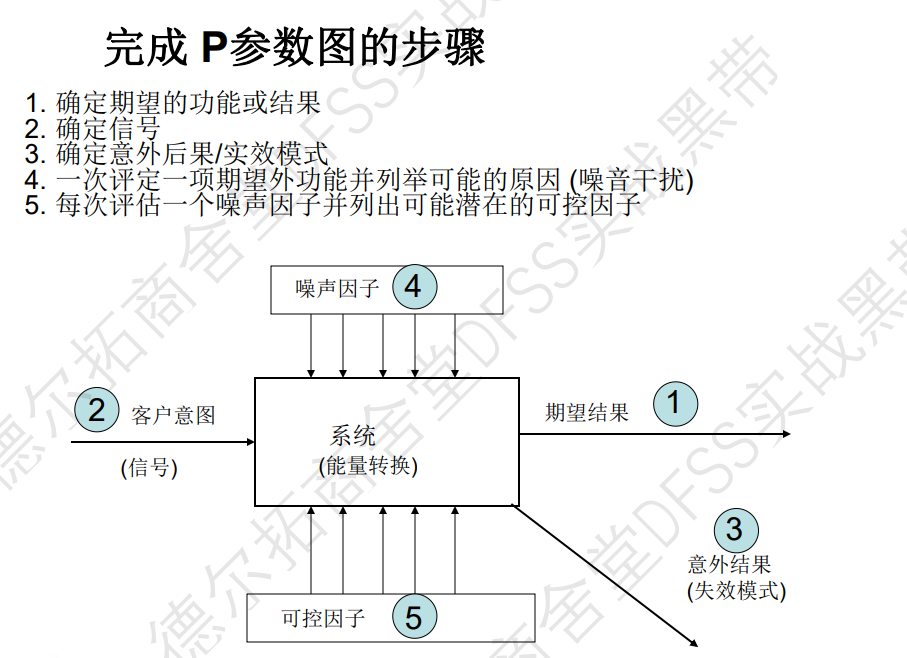
- 五种常见的功能失效模式(TRIZ中也有类似的功能分析):功能缺失、功能不足、功能过剩、功能频繁出错、副作用、随时间衰退

- 结构框图(Block diagram)
- FMEA关注的声音:供应商、客户、公司内部; PL组建一个跨功能团队,同时考虑供应商和客户的风险,使产品更系统得规避风险。
- 失效模式FM,失效后果,失效原因的关系: 模式,使用者的影响,原因(软件、硬件、人的原因)

- 分析根原因的工具:5WHY,因果分析

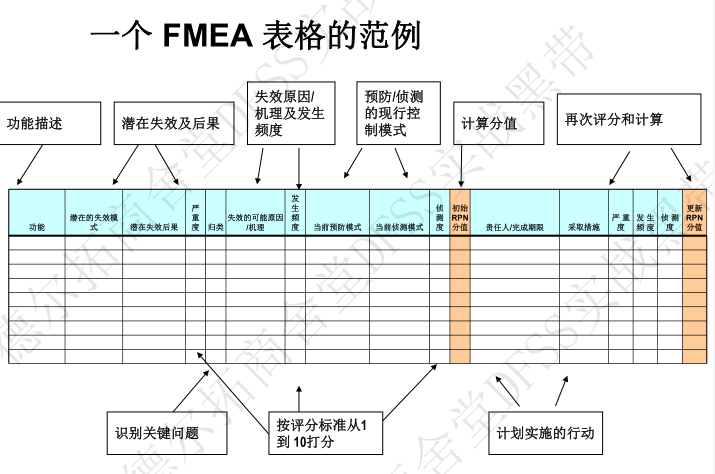
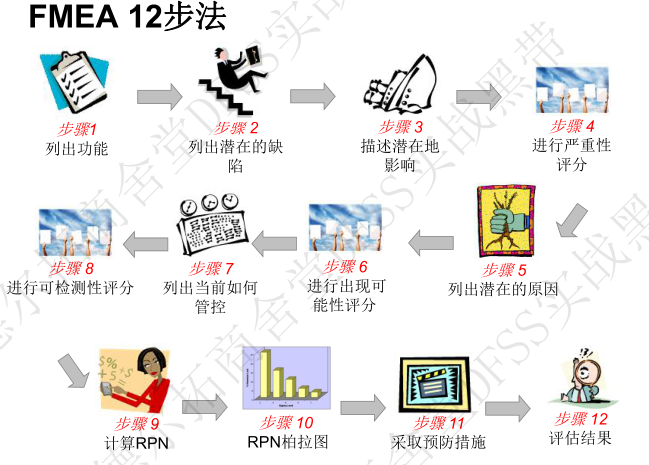


3.5 TRIZ和普氏矩阵 (第27讲) 暂略
2023-7-15 完成3.3部分总结
2023-7-24 快速梳理第26讲 FMEA,发布;不要忘记附加资料中的模板文件,工作上可以直接使用。